
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЁбOЕФАыОЖЮЊ1ЃЌAЃЌBЮЊЁбOЭтСНЕуЃЌAB=1ЃЎИјГіШчЯТЖЈвхЃКЦНвЦЯпЖЮABЃЌЕУЕНЁбOЕФЯв
жаЃЌЁбOЕФАыОЖЮЊ1ЃЌAЃЌBЮЊЁбOЭтСНЕуЃЌAB=1ЃЎИјГіШчЯТЖЈвхЃКЦНвЦЯпЖЮABЃЌЕУЕНЁбOЕФЯв![]() ЃЈ
ЃЈ![]() ЗжБ№ЮЊЕуAЃЌBЕФЖдгІЕуЃЉЃЌЯпЖЮ
ЗжБ№ЮЊЕуAЃЌBЕФЖдгІЕуЃЉЃЌЯпЖЮ![]() ГЄЖШЕФзюаЁжЕГЦЮЊЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЃЎ
ГЄЖШЕФзюаЁжЕГЦЮЊЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЃЎ
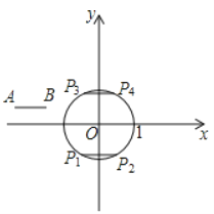
ЃЈ1ЃЉШчЭМЃЌЦНвЦЯпЖЮABЕНЁбOЕФГЄЖШЮЊ1ЕФЯв![]() КЭ
КЭ![]() ЃЌдђетСНЬѕЯвЕФЮЛжУЙиЯЕЪЧ ЃЛдкЕу
ЃЌдђетСНЬѕЯвЕФЮЛжУЙиЯЕЪЧ ЃЛдкЕу![]() жаЃЌСЌНгЕуAгыЕу ЕФЯпЖЮЕФГЄЖШЕШгкЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЃЛ
жаЃЌСЌНгЕуAгыЕу ЕФЯпЖЮЕФГЄЖШЕШгкЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЃЛ
ЃЈ2ЃЉШєЕуAЃЌBЖМдкжБЯп![]() ЩЯЃЌМЧЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЮЊ
ЩЯЃЌМЧЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЃЈ3ЃЉШєЕуAЕФзјБъЮЊ![]() ЃЌМЧЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЮЊ
ЃЌМЧЯпЖЮABЕНЁбOЕФЁАЦНвЦОрРыЁБЮЊ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЦНааЃЌP3ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОндВЕФаджЪМАЁАЦНвЦОрРыЁБЕФЖЈвхЬюПеМДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуOзїOEЁЭABгкЕуEЃЌНЛЯвCDгкЕуFЃЌЗжБ№ЧѓГіOEЁЂOFЕФГЄЃЌгЩ![]() ЕУЕН
ЕУЕН![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЃЈ3ЃЉЯпЖЮABЕФЮЛжУБфЛЛЃЌПЩвдПДзїЪЧвдЕуA![]() ЮЊдВаФЃЌАыОЖЮЊ1ЕФдВЃЌжЛашдкЁбOФкевЕНгыжЎЦНааЃЌЧвГЄЖШЮЊ1ЕФЯвМДПЩЃЎЦНвЦОрРы
ЮЊдВаФЃЌАыОЖЮЊ1ЕФдВЃЌжЛашдкЁбOФкевЕНгыжЎЦНааЃЌЧвГЄЖШЮЊ1ЕФЯвМДПЩЃЎЦНвЦОрРы![]() ЕФзюДѓжЕМДЕуAЃЌBЕуЕФЮЛжУЃЌгЩДЫЕУГі
ЕФзюДѓжЕМДЕуAЃЌBЕуЕФЮЛжУЃЌгЩДЫЕУГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉЦНааЃЛP3ЃЛ
ЃЈ2ЃЉШчЭМЃЌЯпЖЮABдкжБЯп![]() ЩЯЃЌЦНвЦжЎКѓгыдВЯрНЛЃЌЕУЕНЕФЯвЮЊCDЃЌCDЁЮABЃЌЙ§ЕуOзїOEЁЭABгкЕуEЃЌНЛЯвCDгкЕуFЃЌOFЁЭCDЃЌСю
ЩЯЃЌЦНвЦжЎКѓгыдВЯрНЛЃЌЕУЕНЕФЯвЮЊCDЃЌCDЁЮABЃЌЙ§ЕуOзїOEЁЭABгкЕуEЃЌНЛЯвCDгкЕуFЃЌOFЁЭCDЃЌСю![]() ЃЌжБЯпгыxжсНЛЕуЮЊЃЈ-2ЃЌ0ЃЉЃЌжБЯпгыxжсМаНЧЮЊ60ЁуЃЌЁр
ЃЌжБЯпгыxжсНЛЕуЮЊЃЈ-2ЃЌ0ЃЉЃЌжБЯпгыxжсМаНЧЮЊ60ЁуЃЌЁр![]() ЃЎ
ЃЎ
гЩДЙОЖЖЈРэЕУЃК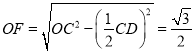 ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
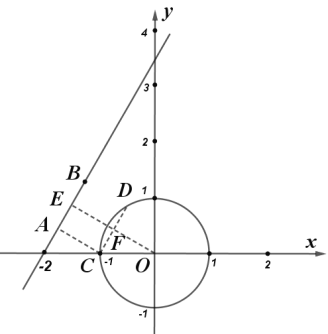
ЃЈ3ЃЉЯпЖЮABЕФЮЛжУБфЛЛЃЌПЩвдПДзїЪЧвдЕуA![]() ЮЊдВаФЃЌАыОЖЮЊ1ЕФдВЃЌжЛашдкЁбOФкевЕНгыжЎЦНааЃЌЧвГЄЖШЮЊ1ЕФЯвМДПЩЃЛ
ЮЊдВаФЃЌАыОЖЮЊ1ЕФдВЃЌжЛашдкЁбOФкевЕНгыжЎЦНааЃЌЧвГЄЖШЮЊ1ЕФЯвМДПЩЃЛ
ЕуAЕНOЕФОрРыЮЊ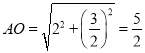 ЃЎ
ЃЎ
ШчЭМЃЌЦНвЦОрРы![]() ЕФзюаЁжЕМДЕуAЕНЁбOЕФзюаЁжЕЃК
ЕФзюаЁжЕМДЕуAЕНЁбOЕФзюаЁжЕЃК![]() ЃЛ
ЃЛ
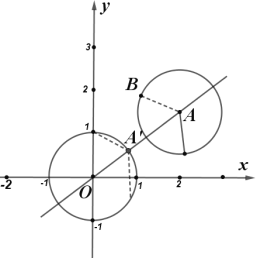
ЦНвЦОрРы![]() ЕФзюДѓжЕЯпЖЮЪЧЯТЭМABЕФЧщПіЃЌМДЕБA1,A2ЙигкOAЖдГЦЃЌЧвA1B2ЁЭA1A2ЧвA1B2=1ЪБ.ЁЯB2A2A1=60ЁуЃЌдђЁЯOA2A1=30Ёу,
ЕФзюДѓжЕЯпЖЮЪЧЯТЭМABЕФЧщПіЃЌМДЕБA1,A2ЙигкOAЖдГЦЃЌЧвA1B2ЁЭA1A2ЧвA1B2=1ЪБ.ЁЯB2A2A1=60ЁуЃЌдђЁЯOA2A1=30Ёу,
ЁпOA2=1,ЁрOM=![]() , A2M=
, A2M=![]() ,
,
ЁрMA=3,AA2=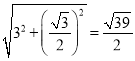 ,
,
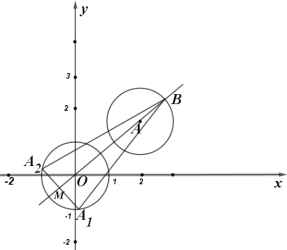
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊЃК
ЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ


 зжДЪОфЦЊгыЭЌВНзїЮФДяБъЯЕСаД№АИ
зжДЪОфЦЊгыЭЌВНзїЮФДяБъЯЕСаД№АИ зпНјЮФбдЮФЯЕСаД№АИ
зпНјЮФбдЮФЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌвд
ЃЌвд![]() ЮЊдВаФЃЌвд
ЮЊдВаФЃЌвд![]() ЕФГЄЮЊАыОЖЛЛЁЃЌдйвдЯпЖЮ
ЕФГЄЮЊАыОЖЛЛЁЃЌдйвдЯпЖЮ![]() ЕФжаЕуPЮЊдВаФЃЌвд
ЕФжаЕуPЮЊдВаФЃЌвд![]() ЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуAЃЌСЌНг
ЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуAЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕуBЃЌЙ§ЕуBзї
гкЕуBЃЌЙ§ЕуBзї![]() ЕФЦНааЯп
ЕФЦНааЯп![]() НЛ
НЛ![]() гкЕуCЃЎ
гкЕуCЃЎ
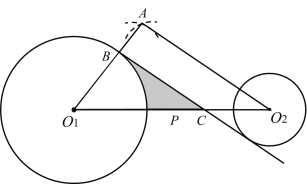
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕРЯАхОгЊМзЁЂввСНИіЗўзАЕъЦЬЃЌУПИіЕъЦЬИїдкЭЌвЛЖЮЪБМфФкЖМФмЪлГіAЁЂBСНжжПюЪНЕФЗўзАКЯМЦ30МўЧвМзЕъЪл1МўAПюКЭ2МўBПюПЩЛёЕУ110дЊЃЌЪл2МўAКЭ1МўBПЩЛёЕУ100дЊЃЌввЕъУПЪлГівЛМўAПюЛёЕУ27дЊЃЌ1МўBПюЛёРћ36дЊЃЌ
ЃЈ1ЃЉЮЪдкМзЕъЪлГі1МўAКЭ1МўBЗжБ№ЛёРћЖрЩйдЊЃП
ЃЈ2ЃЉФГШеЭѕРЯАхНјСЫAПюЪНЕФЗўзА35МўЃЌBПюЪНЕФЗўзА25МўЃЌШчЙћЗжХфИјМзЕъЕФAПюЪНЕФЗўзАxМўЃЌЂйЧѓЭѕРЯАхЛёШЁЕФРћШѓyЃЈдЊЃЉгыxЃЈМўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЂкгЩгкМзЁЂввСНИіЕъЦЬЫљДІЕФЕиЖЮдвђЃЌЭѕРЯАхЯыдкБЃжЄввЕъРћШѓВЛаЁгк950дЊЕФЧАЬсЯТЃЌЪЙЕУздМКЛёШЁЕФРћШѓзюДѓЃЌЧыФуАяЭѕРЯАхЩшМЦвЛжжзюМбЗжХфЗНАИЃЌВЂЧѓзюДѓЕФзмРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
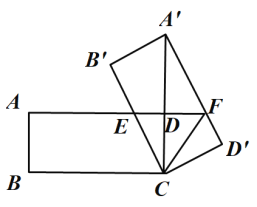
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌ AB=3ЃЌBC=4ЃЌНЋОиаЮABCDШЦЕуCа§зЊЃЌЕуAЁЂBЁЂDЕФЖдгІЕуЗжБ№ЮЊAЁЏ ЁЂBЁЏЁЂ DЁЏЃЌЕБAЁЏ ТфдкБпCDЕФбгГЄЯпЩЯЪБЃЌБпAЁЏ DЁЏ гыБп ADЕФбгГЄЯпНЛгкЕуFЃЌСЊНсCFЃЌФЧУДЯпЖЮCFЕФГЄЖШЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
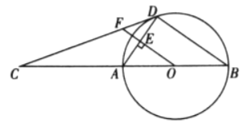
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЮЊBAбгГЄЯпЩЯвЛЕуЃЌCDЪЧЁбOЕФЧаЯпЃЌDЮЊЧаЕуЃЌOFЁЭADгкЕуEЃЌНЛCDгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯADC=ЁЯAOFЃЛ
ЃЈ2ЃЉШєsinC=![]() ЃЌBD=8ЃЌЧѓEFЕФГЄЃЎ
ЃЌBD=8ЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙудЊЪаФГжабЇОйааСЫЁАНћЖОжЊЪЖОКШќЁБЃЌЭѕРЯЪІНЋОХФъМЖЃЈ1ЃЉАрбЇЩњГЩМЈЛЎЗжЮЊAЁЂBЁЂCЁЂDЁЂEЮхИіЕШМЖЃЌВЂЛцжЦСЫЭМ1ЁЂЭМ2СНИіВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжаЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
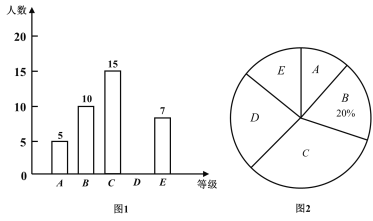
ЃЈ1ЃЉЧѓОХФъМЖЃЈ1ЃЉАрЙВгаЖрЩйУћЭЌбЇЃП
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЌВЂМЦЫуЩШаЮЭГМЦЭМжаЕФЁАCЁБЫљЖдгІЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉГЩМЈЮЊAРрЕФ5УћЭЌбЇжаЃЌга2УћФаЩњКЭ3УћХЎЩњЃЛЭѕРЯЪІЯыДгет5УћЭЌбЇжаШЮбЁ2УћЭЌбЇНјааНЛСїЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓбЁШЁЕФ2УћЭЌбЇЖМЪЧХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСаЗНГЬЛђЗНГЬзщНтгІгУЬтЃК
ФГаЃГѕЖўФъМЖЕФЭЌбЇГЫзјДѓАЭГЕШЅББОЉеЙРРЙнВЮЙлЁАэЦэТЗмНјЕФЮхФъЁБДѓаЭГЩОЭеЙЃЌББОЉеЙРРЙнОрРыИУаЃ12ЧЇУзЃЌ1КХГЕГіЗЂ3ЗжжгКѓЃЌ2КХГЕВХГіЗЂЃЌНсЙћСНГЕЭЌЪБЕНДяЃЌвбжЊ2КХГЕЕФЦНОљЫйЖШЪЧ1КХГЕЕФЦНОљЫйЖШЕФ1.2БЖЃЌЧѓ2КХГЕЕФЦНОљЫйЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаТНЈаЁЧјвЊаовЛЬѕ1050УзГЄЕФТЗЃЌМзЁЂввСНИіЙЄГЬЖгЯыГаНЈетЯюЙЄГЬЃЎО
СЫНтЕУЕНвдЯТаХЯЂЃЈШчБэЃЉЃК
ЙЄГЬЖг | УПЬьаоТЗЕФГЄЖШЃЈУзЃЉ | ЕЅЖРЭъГЩЫљашЬьЪ§ЃЈЬьЃЉ | УПЬьЫљашЗбгУЃЈдЊЃЉ |
МзЖг | 30 | n | 600 |
ввЖг | m | nЉ14 | 1160 |
ЃЈ1ЃЉМзЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЬьЪ§n=ЁЁЁЁЃЌввЖгУПЬьаоТЗЕФГЄЖШm=ЁЁЁЁЃЈУзЃЉЃЛ
ЃЈ2ЃЉМзЖгЯШаоСЫxУзжЎКѓЃЌМзЁЂввСНЖгвЛЦ№аоТЗЃЌгжгУСЫyЬьЭъГЩетЯюЙЄГЬЃЈЦфжаxЃЌyЮЊе§ећЪ§ЃЉЃЎ
ЂйЕБx=90ЪБЃЌЧѓГіввЖгаоТЗЕФЬьЪ§ЃЛ
ЂкЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛгУаДГіxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЂлШєзмЗбгУВЛГЌЙ§22800дЊЃЌЧѓМзЖгжСЩйЯШаоСЫЖрЩйУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌзуЧђГЁЩЯЪиУХдБдкOДІПЊГівЛИпЧђЃЌЧђДгРыЕиУц1УзЕФAДІЗЩГіЃЈAдкyжсЩЯЃЉЃЌдЫЖЏдБввдкОрOЕу6УзЕФBДІЗЂЯжЧђдкздМКЭЗЕФе§ЩЯЗНДяЕНзюИпЕуMЃЌОрЕиУцдМ4УзИпЃЌЧђТфЕиКѓгжвЛДЮЕЏЦ№ЃЌОнЪдбщВтЫуЃЌзуЧђдкВнЦКЩЯЕЏЦ№КѓЕФХзЮяЯпгыдРДЕФХзЮяЯпаЮзДЯрЭЌЃЌзюДѓИпЖШМѕЩйЕНдРДзюДѓИпЖШЕФвЛАыЃЎ
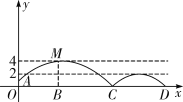
ЃЈ1ЃЉЧѓзуЧђПЊЪМЗЩГіЕНЕквЛДЮТфЕиЪБЃЌИУХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉзуЧђЕквЛДЮТфЕиЕуCОрЪиУХдБЖрЩйУзЃПЃЈШЁ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉдЫЖЏдБвввЊЧРЕНзуЧђЕкЖўИіТфЕуDЃЌЫћгІдйЯђЧАХмЖрЩйУзЃПЃЈШЁ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com