
【题目】如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.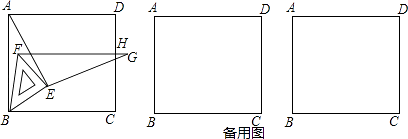
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求 ![]() 的值.
的值.
【答案】
(1)
证明:在△ABE和△GFE中,
 ,
,
∴△ABE≌△GFE
(2)
解:∵△ABE≌△GFE,
∴∠BAE=∠BGN,
∵∠AMN=∠EMG,
∴∠ANM=∠MEG=90°,
∴MH⊥AB,
同理得,DH=AN,
要使DH最小,则BN最大,
∵BN≤BF,
∴当BF与BN重合时,AN最小,
∴∠ABE=∠FBE=45°
(3)
解:在△APE和△ECG中,
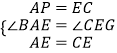 ,
,
∴△APE≌△ECG,
∴GH=BF,
∴∠ECG=APE=135°
∴△HCG是等腰直角三角形,
∴HG=CH=FE,
∴ ![]() ,
,
∵FG=AB=BC,
∴HG=BF,
∴ ![]() .
.
【解析】(1)由等腰直角三角板和正方形ABCD的特点,直接得到△ABE≌△GFE.(2)由△ABE≌△GFE得到的条件判断出MH⊥AB,再判断DH最小时的位置,即可;(3)由△APE≌△ECG得到结论,判断出△HCG是等腰直角三角形,即可求出结果.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点. 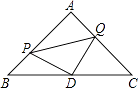
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
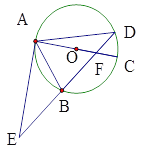
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
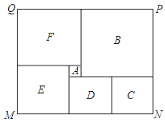
【题目】如图的长方形MNPQ是州某市民健身广场的平面示意图,它是由6个正方形拼成的(分别用A,B,C,D,E,F六个字母表示).已知中间最小的正方形A的边长是1米,设正方形C的边长是x米.
(1)请用含x的代数式分别表示出正方形EF和B的边长;
(2)观察图形的特点,找出两个等量关系,分别用两种方法列方程求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,若甲,乙两个工程队单独铺设分别需要10天和15天完成,如果两队从M处开始,分别沿两个不同方向同时施工![]() 天后,因甲队另有任务,余下的工程由乙队单独施工10天完成,求
天后,因甲队另有任务,余下的工程由乙队单独施工10天完成,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
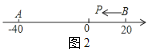
【题目】.A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,我们就称点C是【A,B】的和谐点.例如:图1中,点A表示的数为-1,点B表示的数为2。表示1的点C到点A的距离是2,到点B的距离是1.那么点C是【A,B】的和谐点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的和谐点,但点D是【B,A】的和谐点
(1)若数轴上M,N两点所表示的数分别为![]() 且
且![]() 满足
满足![]() ,请求
,请求
出【M,N】的和谐点表示的数;
(2)如图2,A,B在数轴上表乐的数分别为-40和20,现有一点P从点B出发向左运动
①若点P到达点A停止,则当P点运动多少个单位时P,A,B中恰有一个点为其余两点的和谐点?
②若点P到达点A后继续向左运动,是否存在使得P,A,B中恰有一个点为其余两点的和谐点的情况?若存在,请直接写出此时PB的距离,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形.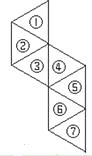
(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于 ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com