
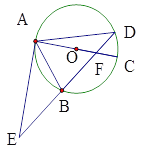
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)、连接CD,根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°,根据同弧所对的圆周角相等得出∠BAC=∠EDC,然后结合已知条件得出∠EAB+∠BAC=90°,从而说明切线;(2)、连接BC,根据直径的性质得出∠ABC=90°,根据B是EF的中点得出AB=EF,即∠BAC=∠AFE,则得出三角形相似;(3)、根据三角形相似得出![]() ,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入
,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入![]() 求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
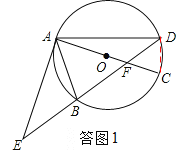
试题解析:(1)、如答图1,连接CD, ∵AC是⊙O的直径,∴∠ADC=90°. ∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切线.
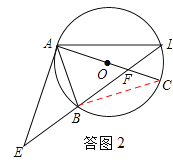
(2)、如答图2,连接BC, ∵AC是⊙O的直径,∴∠ABC=90°. ∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.
(3)、∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有两条边和一个角对应相等的两个三角形全等
B.矩形的对角线互相垂直平分
C.正方形既是轴对称图形又是中心对称图形
D.一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这2名学生立定跳远成绩的( )
A.方差B.平均数C.频率分布D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
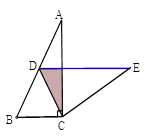
【题目】如图,在Rt△ABC中,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时点D在AB边上,斜边DE交AC于点F,则n=_______; 图中阴影部分的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正确的结论有 ( )
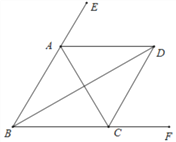
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P(2,1)与点Q(2,﹣1),下列描述正确是( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称 D. 都在y=2x的图象上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.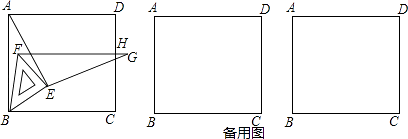
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com