
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点. 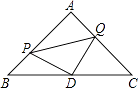
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
【答案】
(1)证明:连接AD
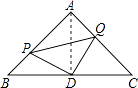
∵△ABC是等腰直角三角形,D是BC的中点
∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,
在△BPD和△AQD中,
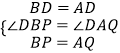 ,
,
∴△BPD≌△AQD(SAS),
∴PD=QD,∠ADQ=∠BDP,
∵∠BDP+∠ADP=90°
∴∠ADP+∠ADQ=90°,即∠PDQ=90°,
∴△PDQ为等腰直角三角形
(2)解:当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:
∵∠BAC=90°,AB=AC,D为BC中点,
∴AD⊥BC,AD=BD=DC,∠B=∠C=45°,
∴△ABD是等腰直角三角形,
当P为AB的中点时,DP⊥AB,即∠APD=90°,
又∵∠A=90°,∠PDQ=90°,
∴四边形APDQ为矩形,
又∵DP=AP= ![]() AB,
AB,
∴矩形APDQ为正方形(邻边相等的矩形为正方形).
【解析】(1)连接AD,根据直角三角形的性质可得AD=BD=DC,从而证明△BPD≌△AQD,得到PD=QD,∠ADQ=∠BDP,则△PDQ是等腰三角形;由∠BDP+∠ADP=90°,得出∠ADP+∠ADQ=90°,得到△PDQ是直角三角形,从而证出△PDQ是等腰直角三角形;(2)若四边形APDQ是正方形,则DP⊥AP,得到P点是AB的中点.
【考点精析】掌握等腰直角三角形和正方形的判定方法是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有两条边和一个角对应相等的两个三角形全等
B.矩形的对角线互相垂直平分
C.正方形既是轴对称图形又是中心对称图形
D.一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
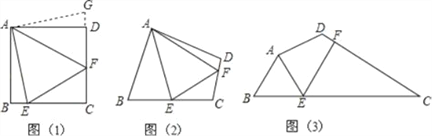
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( ) 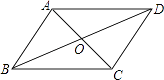
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这2名学生立定跳远成绩的( )
A.方差B.平均数C.频率分布D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.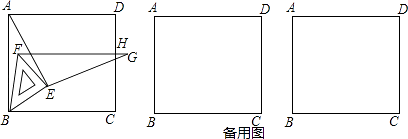
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com