
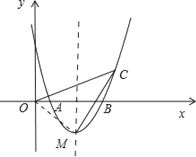
【题目】如图,抛物线![]() 过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
(1)求抛物线的解析式,并写出顶点M的坐标;
(2)连接OC,CM,求sin∠OCM的值;
(3)若点P是抛物线对称轴上的一个动点,求使△PBC为直角三角形点P的坐标.

【答案】(1)抛物线的解析式为![]() ,顶点M的坐标为(2,﹣1);(2)
,顶点M的坐标为(2,﹣1);(2)![]() 的值为
的值为![]() ;(3)点P坐标为P(2,1)或(2,2)或(2,
;(3)点P坐标为P(2,1)或(2,2)或(2,![]() )或(2,
)或(2,![]() ).
).
【解析】
(1)利用待定系数法先求出抛物线的解析式,再根据顶点式的特点可写出顶点坐标;
(2)根据点C和点M的坐标,求出![]() 的长,可得
的长,可得![]() 是直角三角形,再利用正弦的定义即可得;
是直角三角形,再利用正弦的定义即可得;
(3)先可知点P的横坐标为2,设其坐标为![]() ,再根据抛物线的解析式求出点B的坐标,利用两点距离公式分别求出
,再根据抛物线的解析式求出点B的坐标,利用两点距离公式分别求出![]() 的长,最后根据
的长,最后根据![]() 为直角三角形,分三种情况,利用勾股定理求解即可.
为直角三角形,分三种情况,利用勾股定理求解即可.
(1)由抛物线![]() 过点
过点![]() ,得:
,得:
![]() ,解得
,解得![]()
故抛物线的解析式为![]() ,顶点M的坐标为
,顶点M的坐标为![]() ;
;
(2)如图,连接OM
由C和M的坐标,利用勾股定理可得:![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 是直角三角形,且
是直角三角形,且![]()
![]() ;
;
(3)由(1)得抛物线的对称轴为直线![]() ,因此设点P的坐标为
,因此设点P的坐标为![]()
![]() 抛物线交x轴于A、B两点
抛物线交x轴于A、B两点
![]() 令
令![]() 得点A和B的坐标为:
得点A和B的坐标为:![]()
由两点距离公式得:![]()
根据![]() 为直角三角形,分以下三种情况:
为直角三角形,分以下三种情况:
①当![]() 时,则
时,则![]() ,即
,即![]()
解得:![]() 或
或![]()
故点P的坐标为![]() 或
或![]()
②当![]() 时,则
时,则![]() ,即
,即![]()
解得:![]()
故点P的坐标为![]()
③当![]() 时,则
时,则![]() ,即
,即![]()
解得:![]()
故点P的坐标为![]()
综上,点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第8个图形的小圆个数是( )

A.58B.66C.74D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小组做用频率估计概率“的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 掷一枚均匀的正六面体骰子,出现3点朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上,连接
上,连接![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() .
.

(1)若点![]() 是
是![]() 边上的中点,且
边上的中点,且![]() ,求
,求![]() 的值.
的值.
(2)若点![]() 是
是![]() 边上的中点,且
边上的中点,且![]() ,求
,求![]() 的值.(用含
的值.(用含![]() 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)探究三:若![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值(不写解答过程).
的值(不写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 于点
于点![]() ,连
,连![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ..其中正确结论的个数为( )
..其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某旅游公司国庆期间倾情打造了四条旅游路线:A.壶口瀑布,B.平遥古城,C.云冈石窟,D.五台山.
A.  B.
B.  C.
C.  D.
D. 
李老师和张老师都计划在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李老师选择线路A.壶口瀑布的概率是多少?
(2)用画树状图或列表的方法,求李老师和张老师恰好选择同一线路旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
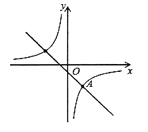
(1)求反比例函数的解析式;
(2)若一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,请直接写出关于x的不等式
,请直接写出关于x的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.

(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com