解:(1)∵点A(2,4)在

的图象上,则k=8,
∴双曲线S
2的解析式为
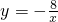
,
设直线AB的解析式为y=ax+b,
则
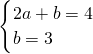
,
∴
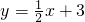
;
∴
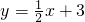
;
(2)由(1)可设P(m,

),
又PE⊥x轴,则E点的横坐标与P点相同为m,
点E在双曲线S
2上,
∴y
E=
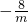
,即E(m,
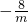
),
∴h=y
E-y
P=
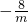
-
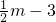
(-6<m<0);
(3)分两种情况:
①若△AEP∽△COB,如图1,
此时,∠AEP=∠COB=90°,即AE⊥EP,
则y
E=y
A=4,x
E=-2;
∴E(-2,4);
又EP⊥x轴,则x
P=x
E=-2,
y
P=

x
P+3=

×(-2)+3=2;
∴P(-2,2);
②若△EAP∽△COB,如图2,
此时∠EAP=∠COB=90°,过点A作AF⊥EP于F,
则有△EFA∽△COB,
∴
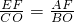
;
对于直线y=

;
当y=0时,x=-6,
则C(-6,0);
∴OC=6;
又P点的坐标为(m,

),则E(m,
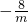
),F(m,4),
∴EF=

,AF=2-m;
可得:

,解得:m
2-4m-4=0;
∴m
1=2-2

,m
2=2+2

;
∴m=2-2

;
∴

∴
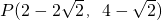
.
综上所述,存在点P(-2,2)或(2-2

,4-

),使得以P、E、A为顶点的三角形与△BOC相似.

分析:(1)由A点坐标易求k值,再根据翻折的特点求出双曲线S
2的解析式;根据A、B两点坐标求直线解析式;
(2)根据PE=E点纵坐标-P点纵坐标,求h与m之间的函数关系式;
(3)△BOC为直角三角形,而∠EPA不是直角,所以另外两个角可能是直角,分两种情形讨论.
点评:本题考查反比例函数和一次函数解析式的确定,要注意(3)在相似形中需根据对应关系分情形讨论.

 如图,已知点A(2,4)在反比例函数
如图,已知点A(2,4)在反比例函数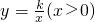 的图象S1上,将双曲线S1沿y轴翻折后得到的是反比例函数
的图象S1上,将双曲线S1沿y轴翻折后得到的是反比例函数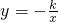 的图象S2,直线AB交y轴于点B(0,3),交x轴于点C,P为线段BC上的一个动点(点P与B、C不重合),过P作x轴的垂线与双曲线S2在第二象限相交于点E.
的图象S2,直线AB交y轴于点B(0,3),交x轴于点C,P为线段BC上的一个动点(点P与B、C不重合),过P作x轴的垂线与双曲线S2在第二象限相交于点E. 的图象上,则k=8,
的图象上,则k=8,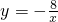 ,
,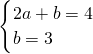 ,
,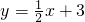 ;
;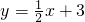 ;
; ),
),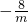 ,即E(m,
,即E(m,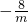 ),
),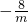 -
-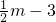 (-6<m<0);
(-6<m<0); xP+3=
xP+3= ×(-2)+3=2;
×(-2)+3=2;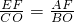 ;
; ;
; ),则E(m,
),则E(m,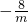 ),F(m,4),
),F(m,4), ,AF=2-m;
,AF=2-m; ,解得:m2-4m-4=0;
,解得:m2-4m-4=0; ,m2=2+2
,m2=2+2 ;
; ;
;
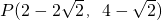 .
. ,4-
,4- ),使得以P、E、A为顶点的三角形与△BOC相似.
),使得以P、E、A为顶点的三角形与△BOC相似.


 智能训练练测考系列答案
智能训练练测考系列答案 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设