
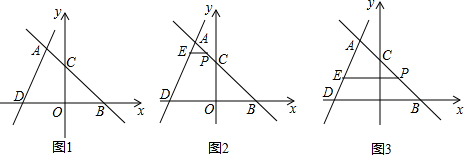
ЗжЮі ЃЈ1ЃЉИљОнжБЯпABНЛxжсе§АыжсгкЕуBЃЌНЛyжсгкЕуCЃЌOB=OCЃЌЩшГіНтЮіЪНЮЊy=-x+nЃЌАбAЕФзјБъДњШыЧѓЕУnЕФжЕЃЌДгЖјЧѓЕУBЕФзјБъЃЌдйИљОнШ§НЧаЮЕФУцЛ§НЈСЂЗНГЬЧѓГіBDЕФжЕЃЌЧѓГіODЕФжЕЃЌДгЖјЧѓГіDЕуЕФзјБъЃЌжБНгИљОнД§ЖЈЯЕЪ§ЗЈЧѓГіADЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЯШИљОнBЁЂAЕФзјБъЧѓГіжБЯпABЕФНтЮіЪНЃЌНЋPЕуЕФКсзјБъДњШыжБЯпABЕФНтЮіЪНЃЌЧѓГіPЕФзмзјБъЃЌНЋPЕуЕФзмзјБъДњШыжБЯпADЕФНтЮіЪНОЭПЩвдЧѓГіEЕФКсзјБъЃЌИљОнЯпЖЮЕФКЭВюЙиЯЕОЭПЩвдЧѓГіНсТлЃЛ
ЃЈ3ЃЉвЊЪЙЁїPEFЮЊЕШбќжБНЧШ§НЧаЮЃЌЗжШ§жжЧщПіЗжБ№вдЕуPЁЂEЁЂFЮЊжБНЧЖЅЕуЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЧѓГіЃЈ2ЃЉжаmЕФжЕЃЌОЭПЩвдЧѓГіFЕуЕФзјБъЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпOB=OCЃЌ
ЁрЩшжБЯпABЕФНтЮіЪНЮЊy=-x+nЃЌ
ЁпжБЯпABОЙ§AЃЈ-2ЃЌ6ЃЉЃЌ
Ёр2+n=6ЃЌ
Ёрn=4ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊy=-x+4ЃЌ
ЁрBЃЈ4ЃЌ0ЃЉЃЌ
ЁрOB=4ЃЌ
ЁпЁїABDЕФУцЛ§ЮЊ27ЃЌAЃЈ-2ЃЌ6ЃЉЃЌ
ЁрSЁїABD=$\frac{1}{2}$ЁСBDЁС6=27ЃЌ
ЁрBD=9ЃЌ
ЁрOD=5ЃЌ
ЁрDЃЈ-5ЃЌ0ЃЉЃЌ
ЩшжБЯпADЕФНтЮіЪНЮЊy=ax+bЃЌ
Ёр$\left\{\begin{array}{l}{-2a+b=6}\\{-5a+b=0}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{a=2}\\{b=10}\end{array}\right.$ЃЎ
ЁржБЯпADЕФНтЮіЪНЮЊy=2x+10ЃЛ
ЃЈ2ЃЉЁпЕуPдкABЩЯЃЌЧвКсзјБъЮЊmЃЌ
ЁрPЃЈmЃЌ-m+4ЃЉЃЌ
ЁпPEЁЮxжсЃЌ
ЁрEЕФзнзјБъЮЊ-m+4ЃЌ
ДњШыy=2x+10ЕУЃЌ-m+4=2x+10ЃЌ
НтЕУx=$\frac{-m-6}{2}$ЃЌ
ЁрEЃЈ$\frac{-m-6}{2}$ЃЌ-m+4ЃЉЃЌ
ЁрPEЕФГЄy=m-$\frac{-m-6}{2}$=$\frac{3}{2}$m+3ЃЛ
МДy=$\frac{3}{2}$m+3ЃЌЃЈ0ЃМmЃМ4ЃЉЃЌ
ЃЈ3ЃЉдкxжсЩЯДцдкЕуFЃЌЪЙЁїPEFЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЂйЕБЁЯFPE=90ЁуЪБЃЌШчЭМЂйЃЌ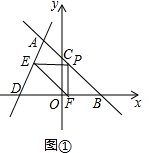
гаPF=PEЃЌPF=-m+4 PE=$\frac{3}{2}$m+3ЃЌ
Ёр-m+4=$\frac{3}{2}$m+3ЃЌ
НтЕУm=$\frac{2}{5}$ЃЌДЫЪБFЃЈ$\frac{2}{5}$ЃЌ0ЃЉЃЛ
ЂкЕБЁЯPEF=90ЁуЪБЃЌШчЭМЂкЃЌгаEP=EFЃЌEFЕФГЄЕШгкЕуEЕФзнзјБъЃЌ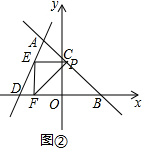
ЁрEF=-m+4ЃЌ
ЁрЁр-m+4=$\frac{3}{2}$m+3ЃЌ
НтЕУЃКm=$\frac{2}{5}$ЃЎ
ЁрЕуEЕФКсзјБъЮЊx=$\frac{-m-6}{2}$=-$\frac{16}{5}$ЃЌ
ЁрFЃЈ-$\frac{16}{5}$ЃЌ0ЃЉЃЛ
ЂлЕБЁЯPFE=90ЁуЪБЃЌШчЭМЂлЃЌга FP=FEЃЌ
ЁрЁЯFPE=ЁЯFEPЃЎ
ЁпЁЯFPE+ЁЯEFP+ЁЯFEP=180ЁуЃЌ
ЁрЁЯFPE=ЁЯFEP=45ЁуЃЎ
зїFRЁЭPEЃЌЕуRЮЊДЙзуЃЌ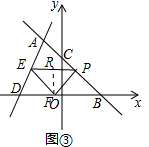
ЁрЁЯPFR=180Ёу-ЁЯFPE-ЁЯPRF=45ЁуЃЌ
ЁрЁЯPFR=ЁЯRPFЃЌ
ЁрFR=PRЃЎ
ЭЌРэFR=ERЃЌ
ЁрFR=$\frac{1}{2}$PEЃЎ
ЁпЕуRгыЕуEЕФзнзјБъЯрЭЌЃЌ
ЁрFR=-m+4ЃЌ
Ёр-m+4=$\frac{1}{2}$ЃЈ$\frac{3}{2}$m+3ЃЉЃЌ
НтЕУЃКm=$\frac{10}{7}$ЃЌ
ЁрPR=FR=-m+4=-$\frac{10}{7}$+4=$\frac{18}{7}$ЃЌ
ЁрЕуFЕФКсзјБъЮЊ$\frac{10}{7}$-$\frac{18}{7}$=-$\frac{8}{7}$ЃЌ
ЁрFЃЈ-$\frac{8}{7}$ЃЌ0ЃЉЃЎ
злЩЯЃЌдкxжсЩЯДцдкЕуFЪЙЁїPEFЮЊЕШбќжБНЧШ§НЧаЮЃЌЕуFЕФзјБъЮЊЃЈ$\frac{2}{5}$ЃЌ0ЃЉЛђЃЈ-$\frac{16}{5}$ЃЌ0ЃЉЛђЃЈ-$\frac{8}{7}$ЃЌ0ЃЉЃЎ
ЕуЦР БОЬтПМВщСЫЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌШ§НЧаЮЕФУцЛ§ЙЋЪНЕФдЫгУЃЌД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЕФдЫгУЃЌНтД№БОЬтЪБЧѓГіКЏЪ§ЕФНтЮіЪНЪЧЙиМќЃЎ


 ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ІаЪЧздБфСП | BЃЎ | ІаКЭrЖМЪЧздБфСП | CЃЎ | CЪЧІаЕФздБфСП | DЃЎ | CЪЧrЕФздБфСП |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
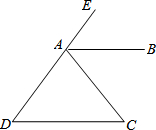 ШчЭМЫљЪОЃЌвЊЯыХаЖЯABгыCDЪЧЗёЦНааЃЌЮвУЧгаФФаЉЗНЗЈЃЈСНжБЯпЦНааЕФЬѕМўЃЉЃЌЧыФуаДГіШ§жжЗНАИЃЌВЂЫЕУїРэгЩЃЎ
ШчЭМЫљЪОЃЌвЊЯыХаЖЯABгыCDЪЧЗёЦНааЃЌЮвУЧгаФФаЉЗНЗЈЃЈСНжБЯпЦНааЕФЬѕМўЃЉЃЌЧыФуаДГіШ§жжЗНАИЃЌВЂЫЕУїРэгЩЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com