
 在平面直角坐标系中有一矩形ABCD,其中A(0,0),B(8,0),D(0,4),若将△ABC沿AC所在直线对折,点B落在点E处,则M点的坐标是(3,4),点E的纵坐标($\frac{24}{5}$,$\frac{32}{5}$).
在平面直角坐标系中有一矩形ABCD,其中A(0,0),B(8,0),D(0,4),若将△ABC沿AC所在直线对折,点B落在点E处,则M点的坐标是(3,4),点E的纵坐标($\frac{24}{5}$,$\frac{32}{5}$). 分析 作△MEC的高线EF,要想求M的坐标就需要求DM的长即可,设DM=x,利用勾股定理列方程可以求出x=3,写出M的坐标;
要想求E的坐标,就需要求DF和EF的长,利用面积法求EF=$\frac{12}{5}$,则可以求出DF和点E的纵坐标,写出点E的坐标即可.
解答  解:由对折得:∠BAC=∠CAE,
解:由对折得:∠BAC=∠CAE,
∵四边形ABCD为矩形,
∴CD∥AB,
∴∠DCA=∠CAB,
∴∠DCA=∠CAE,
∴AM=CM,
∵B(8,0),D(0,4),
∴AD=4,AB=CD=8,
设DM=x,则AM=CM=8-x,
在Rr△ADM中,DM2+AD2=AM2,
∴x2+42=(8-x)2,
x=3,
∴DM=3,AM=CM=8-3=5,
∴M(3,4),
过E作EF⊥CD于F,
由折叠得:EC=BC=4,
在Rt△MEC中,ME=3,
∴S△MEC=$\frac{1}{2}$ME•EC=$\frac{1}{2}$MC•EF,
∴3×4=5EF,
∴EF=$\frac{12}{5}$,
由勾股定理得:FM=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,
∴DF=3+$\frac{9}{5}$=$\frac{24}{5}$,
∴E($\frac{24}{5}$,$\frac{32}{5}$),
故答案为:(3,4);($\frac{24}{5}$,$\frac{32}{5}$).
点评 本题考查了矩形的性质和翻折变换问题,明确折叠前后的两边及两角对应相等,并熟练掌握矩形的性质,设未知数,利用勾股定理列方程可以求边长,另外本题还运用了面积法求直角三角形斜边上的高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 0或2 | C. | 2或-2 | D. | 0,2或-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:判断题
( 6分) 已知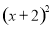 +
+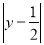 =0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{2}{3}}$xyz与$\sqrt{\frac{2}{3}}$xy是同类项 | B. | $\frac{1}{x}$和2x是同类项 | ||
| C. | -0.5x3y2和2x2y3是同类项 | D. | 5m2n和-2nm2是同类项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com