Question

【题目】等腰三角形一腰长为5，一边上的高为3，则底边长为 ．

Answer 1

【答案】8或 或3
【解析】解：如图所示：

当等腰三角形为锐角三角形，且CD为腰上的高时，

在Rt△ACD中，AC=5，CD=3，

根据勾股定理得：AD= =4，

∴BD=AB﹣AD=5﹣4=1，

在Rt△BDC中，CD=3，BD=1，

根据勾股定理得：BC= = ；

当等腰三角形为钝角三角形，且CD为腰上的高时，

在Rt△ACD中，AC=5，CD=3，

根据勾股定理得：AD= =4，

∴BD=AB+AD=5+4=9，

在Rt△BDC中，CD=3，BD=9，

根据勾股定理得：BC= =3 ；

当AD为底边上的高时，如图所示：

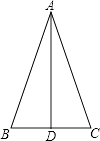
∵AB=AC，AD⊥BC，

∴BD=CD，

在Rt△ABD中，AD=3，AB=5，

根据勾股定理得：BD= =4，

∴BC=2BD=8，

综上，等腰三角形的底边长为8或 或3 ．

所以答案是：8或 或3

【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．