
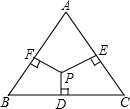
 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,求点P到三角形的三边的距离之和PD+PE+PF的值.
如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,求点P到三角形的三边的距离之和PD+PE+PF的值. 分析 连接AP、BP、CP,设等边三角形的高为h,分别求出△APC、△APB、△BPC的面积,而三个三角形的面积之和等于△ABC面积,由此等量关系可求出到三角形的三边距离之和PD+PE+PF等于△ABC的高.
解答  解:连接AP、BP、CP,
解:连接AP、BP、CP,
设等边三角形的高为h,如图:
∵正三角形ABC边长为2,
∴h=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵S△BPC=$\frac{1}{2}$BC•DP,
S△APC=$\frac{1}{2}$AC•PE,
S△APB=$\frac{1}{2}$AB•PF,
∴S△ABC==$\frac{1}{2}$BC•DP+$\frac{1}{2}$AC•PE+$\frac{1}{2}$AB•PF,
∵AB=BC=AC,
∴S△ABC=$\frac{1}{2}$BC(DP+EP+FP)=$\frac{1}{2}$BC•h,
∴PD+PF+PE=h=$\sqrt{3}$.
点评 本题考查了等边三角形的性质及三角形的面积公式,难度较大,注意计算正确.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
| A. | 三边相等的三角形是等边三角形 | |
| B. | 三个角相等的三角形是等边三角形 | |
| C. | 有一个角是60°的三角形是等边三角形 | |
| D. | 有两个角是60°的三角形是等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 只有符号不同的两个数是互为相反数 | |
| B. | 互为相反数的两数的和为零 | |
| C. | 在数轴上,互为相反数的两数到原点的距离相等 | |
| D. | 零没有相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两角和一边对应相等的两个三角形全等 | |
| B. | 有两边和一角对应相等的两个三角形全等 | |
| C. | 有两边和其中一边上的中线对应相等的两个三角形全等 | |
| D. | 有一边对应相等的两个等边三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
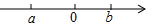 实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b-2a | C. | b | D. | -b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.
如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(-1,m)两点,与x轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com