
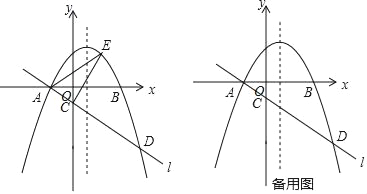
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=kx+h��x���ཻ�ڵ�A����1��0������y���ཻ�ڵ�C����������y=��x2+bx+3��һ����Ϊ��D�������߹�x���ϵ�AB���㣬��CD=4AC��
��1����ֱ��l�������ߵĽ���ʽ��
��2����E��ֱ��l�Ϸ��������ϵ�һ���㣬����ADE������ʱ����E�����ꣻ
��3����P�������߶Գ����ϵ�һ�㣬��Q���������ϣ��ı���APDQ�ܷ�Ϊ���Σ����ܣ���ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��ֱ��l�Ľ���ʽΪy=��x��1����2��E��![]() ��
��![]() ������3��������.
������3��������.
����������������1������ص������������ʽ������⣻
��2������E��EM��x�ᣬ��AD�ڵ�M�����E��m��-m2+2m+3������M��m��-m-1������������ó��������������m�Ķ��κ�������������ֵ���ɣ�
��3���ȸ�������������ı���APDQΪƽ���ı���ʱ��ȷ����P��Q�����꣬�����ù��ɶ������涨�������Ƿ�ֱ���ɣ�
��⣺��1����A��-1��0������y=-x2+bx+3����b=2��
���������ߵĽ���ʽΪy=-x2+2x+3��
����D��DF��x���ڵ�F����ͼ1
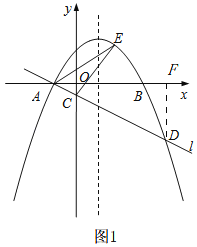
��֤��AOC�ס�AFD��
��![]() ��
��
��CD=4AC��
��![]() ��
��
���D������Ϊ4��
��x=4����y=-x2+2x+3����y=-5��
��D��4��-5����
��x=4��y=-5��x=-1��y=0����y=kx+h��
��ã�k=-1��h=-1��
��ֱ��l�Ľ���ʽΪy=-x-1��
��2������E��EM��x�ᣬ��AD�ڵ�M����ͼ2
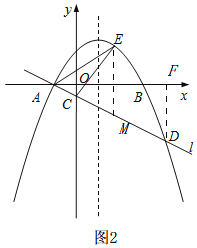
���E��m��-m2+2m+3������M��m��-m-1����
��EM=-m2+2m+3-��-m-1���T-m2+3m+4��
��S��ADE=![]() ��5��-m2+3m+4��=
��5��-m2+3m+4��=![]() m2+
m2+![]() m+10��
m+10��
��m=![]() ʱ����ADE��������
ʱ����ADE��������
��ʱ��E��![]() ��
��![]() ����
����
��3��������
�������£�
�������ߵĶԳ���Ϊֱ��x=1��
��P��1��m����
����AD��ƽ���ı���ADPQ��һ���ߣ���ͼ3
����Q��-4��-21����
m=-21-5=-26����P��1��-26����
��ʱAQ2=32+212=450��QP2=52+52=50��AP2=22+262=680��
��AQ2+QP2��AP2��
���AQP��90�㣬
��ʱƽ���ı���ADPQ���Ǿ��Σ�
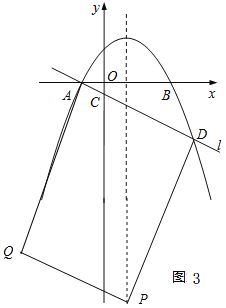
����AD��ƽ���ı���APDQ�ĶԽ��ߣ���ͼ4
����Q��2��3����
m=-5a-3=-8����P��1��-8����
PQ2=12+112=122��PD2=32+32=18QD2=22+82=68��
��PD2+QD2��PQ2��
���PDQ��90�㣬
��ʱƽ���ı���ADPQ���Ǿ��Σ�
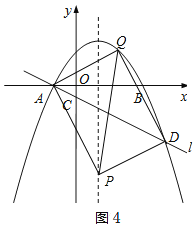
�����������ı���APDQ����Ϊ���Σ�


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ����������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ��������������ôС����Ե�һ����ĸ�����������
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��3���Ӹ��ʵĽǶȷ������㽨��С���ڵڼ���ʹ��������������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������:
��1����ͼ��![]() Ϊֱ�ǣ�
Ϊֱ�ǣ�![]() ����
����![]() ƽ��
ƽ��![]() ƽ��
ƽ��![]() ,��
,��![]() �Ķ�����
�Ķ�����
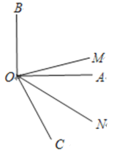
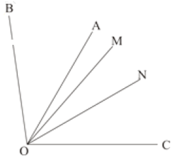
��2����ͼ��![]() ����
����![]() ƽ��
ƽ��![]() ƽ��
ƽ��![]() ��ֱ��д��
��ֱ��д��![]() �Ķ�����
�Ķ�����
��:��1����Ϊ![]() ,����
,����![]() ��
�� ![]()
��Ϊ![]() ƽ��
ƽ��![]() ,����
,����![]() ��
�� ![]() ��
�� ![]()
��Ϊ![]() ƽ��
ƽ��![]() ,����
,����![]() ��
�� ![]() ��
�� ![]()
����![]() ��
�� ![]()
��2��![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�� AFƽ����BAC��BC��AF�� ����ΪE����D���A���ڵ�E�Գƣ�PB�ֱ����߶�CF��AF�ཻ��P��M��

��1����֤��AB=CD��
��2������BAC=2��MPC�������ж���F����MCD��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲���룺
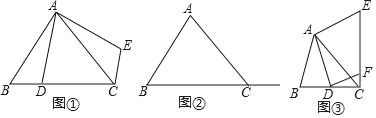
��Rt��ABC�У���BAC=90�㣬AB=AC����D�ڱ�BC�ϣ�����AD������ABD�Ƶ�A��ʱ����ת90������D���ڵ�E������ͼ����ʾ�����߶�CE���߶�BD��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤����
�ڣ�1���������£�����D���߶�BC���ӳ����ϣ����жϣ�1���н����ǻ�����������ͼ���л���ͼ�Σ���֤������жϣ�
��3����չ���죺
��ͼ�ۣ���BAC��90������AB��AC����ACB=45����AC=![]() �������������䣬����D��DF��AD��CE�ڵ�F����ֱ��д���߶�CF���ȵ����ֵ��
�������������䣬����D��DF��AD��CE�ڵ�F����ֱ��д���߶�CF���ȵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�ļ����У�
10��![]() ��3.14��
��3.14��![]() �� 0.6��0�� 75%�� (5)��
�� 0.6��0�� 75%�� (5)��![]() ��
��
�������ϣ�{ ��}��
�������ϣ�{ ��}��
�������ϣ�{ ��}��
���������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����x2��2x��m��1��x���ڵ�A(a��0)��B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ��жϣ��ٵ�x>0ʱ��y>0������a����1����b��4������������������P��x1��y1����Q��x2��y2������x1<1< x2����x1��x2>2����y1> y2���ܵ�C���������߶Գ���ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m��2ʱ���ı���EDFG�ܳ�����СֵΪ![]() ��������ȷ�жϵ�����ǣ� ��
��������ȷ�жϵ�����ǣ� ��

A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
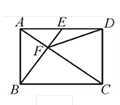
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BE��AC�ڵ�F������AD�ڵ�E������DF������EΪAD���е㣬��DF�ij�Ϊ__________ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѳ�������AE���ۺ��D����BC�ߵĵ�F����BC��5cm��
AB��4cm����1��CF�ij�����2��EF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com