
【题目】如图,AB为圆O的直径,C为圆O上的一点,D为BA延长线上的一点,![]() ,线段DF分别交AC,BC于点E,F,且
,线段DF分别交AC,BC于点E,F,且![]() =45°,圆O的半径为5,
=45°,圆O的半径为5,![]() ,则CF的长( )
,则CF的长( )

A.![]() B.3C.
B.3C.![]() D.4
D.4
科目:初中数学 来源: 题型:
【题目】问题发现:
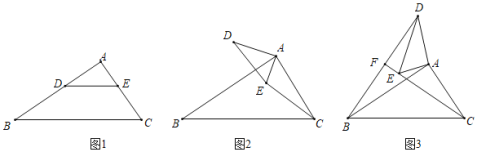
(1)如图1,在Rt△ABC中,∠A=90°,AB=kAC(k>1),D是AB上一点,DE∥BC,则BD,EC的数量关系为 .
类比探究
(2)如图2,将△AED绕着点A顺时针旋转,旋转角为a(0°<a<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由
拓展延伸:
(3)如图3,在(2)的条件下,将△AED绕点A继续旋转,旋转角为a(a>90°).直线BD,CE交于F点,若AC=1,AB=![]() ,则当∠ACE=15°时,BFCF的值为_____.
,则当∠ACE=15°时,BFCF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3的3个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为6,则可获得50元代金券一张;若所得的数字之和为5,则可获得30元代金券一张;若所得的数字之和为4,则可获得15元代金券一张;其它情况都不中奖.
(1)请用列表或树状图的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来.
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
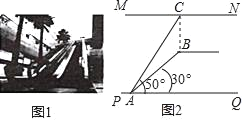
【题目】如图1是某商场从一楼到二楼的自动扶梯,图2是侧面示意图,MN是二楼楼顶,MN∥PQ,点C在MN上,且位于自动扶梯顶端B点的正上方,BC⊥MN.测得AB=10米,在自动扶梯底端A处测得点C的仰角为50°,点B的仰角为30°,求二楼的层高BC(结果保留根号)
(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 同时从点
同时从点![]() 出发,分别沿
出发,分别沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,点
匀速运动,点![]() 到达点
到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 向点
向点![]() 运动,点
运动,点![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 也随之停止.在点
也随之停止.在点![]() 运动过程中,以
运动过程中,以![]() 为边作正方形
为边作正方形![]() 使它与
使它与![]() 在线段
在线段![]() 的同铡.设
的同铡.设![]() 运动的时间为
运动的时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() .
.
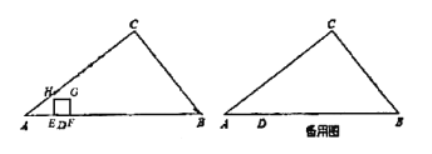
![]() 当
当![]() 时,求正方形
时,求正方形![]() 的顶点刚好落在线段
的顶点刚好落在线段![]() 上时
上时![]() 的值;
的值;
![]() 当
当![]() 时,直接写出当
时,直接写出当![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com