
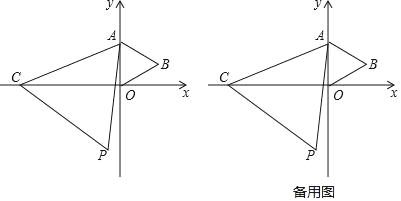
【题目】如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
初步探究
(1)写出点B的坐标 ;
(2)点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;并求出这个图形所对应的函数表达式.
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.
【答案】(1)(![]() ,1);(2)证明见解析;(3)点P在过点B且与AB垂直的直线上,点P所在直线的函数表达式为y=
,1);(2)证明见解析;(3)点P在过点B且与AB垂直的直线上,点P所在直线的函数表达式为y=![]() x﹣2;(4)(﹣2
x﹣2;(4)(﹣2![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣2,0)或(2,0).
,0)或(﹣2,0)或(2,0).
【解析】
(1)如图1中,作BH⊥OA于H.利用等边三角形的性质,解直角三角形求出BH、OH即可;
(2)根据SAS即可判断;
(3)点P在过点B且与AB垂直的直线上.当点P在y轴上时,得P(0,﹣2).由B(![]() ,1).设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入即可解决问题;
,1).设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入即可解决问题;
(4)分四种情形分别求解即可解决问题;
(1)如图1中,作BH⊥OA于H.
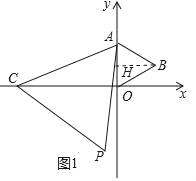
∵△AOB是等边三角形,OA=OB=AB=2,∠BOH=60°
在Rt△OBH中,BH=OBsin60°=![]() ,OH=AH=1,
,OH=AH=1,
∴B(![]() ,1).
,1).
(2)如图2中

∵△AOB与△ACP都是等边三角形,
∴AO=AB,AC=AP,∠CAP=∠OAB=60°,
∴∠CAP+∠PAO=∠OAB+∠PAO,
即∠CAO=∠PAB,
在△AOC与△ABP中,

∴△AOC≌△ABP(SAS).
(3)如图2中,∵△AOC≌△ABP(SAS).
∴∠ABP=∠AOC=90°,
∴PB⊥AB,
∴点P在过点B且与AB垂直的直线上.
当点P在y轴上时,得P(0,﹣2).
∵B(![]() ,1).
,1).
设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入,得
![]()
所以点P所在直线的函数表达式为:y=![]() x﹣2.
x﹣2.
(4)如图3中,
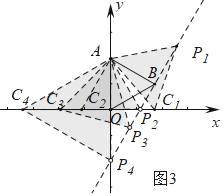
①当OB=BP1=2时,OC1=BP1=2,此时C1(2,0).
②当P2O=P2B时,OC2=BP2=![]() ,此时C2(﹣
,此时C2(﹣,0).
③当OB=BP3=2时,OC3=2,此时C3(﹣2,0).
④当OB=OP4时,OC4=BP4=2![]() ,此时C4(﹣2
,此时C4(﹣2![]() ,0),
,0),
故答案为(﹣2![]() ,0)或(﹣
,0)或(﹣![]()
![]() ,0)或(﹣2,0)或(2,0).
,0)或(﹣2,0)或(2,0).


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】已知多项式2x2+![]() x3+x﹣5x4﹣
x3+x﹣5x4﹣![]() .
.
(1)请指出该多项式是几次几项式,并写出它的二次项、一次项和常数项;
(2)按要求把这个多项式重新排列:①按x的降幂排列;②按x的升幂排列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
(1)求证:AF=BG;
(2)过E点作EH⊥AB于H,试探索线段EH与线段AB的数量关系,并说明理由.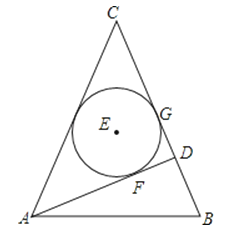
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示-5,点B表示10.动点P从点A出发,沿数轴正方向以每秒1个单位的速度匀速运动;同时,动点Q从点B出发,沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.
(1)当t为 秒时,P,Q两点相遇,求出相遇点所对应的数;
(2)当t为何值时,P,Q两点的距离为3个单位长度,并求出此时点P对应的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-10xy3)·2xy4z;
(2)(-4x)(2x2-2x-1);
(3)0.4x2y·![]() -(-2x)3·xy3;
-(-2x)3·xy3;
(4)-3a![]() +2b(a2-ab)-2a2(b+3).
+2b(a2-ab)-2a2(b+3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,O为原点,现A,B两点分别以1个单位长度/秒的速度同时向左运动。
(1)几秒后,原点恰好在A,B两点正中间?
(2)几秒后,恰好有OA:OB=1:2.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)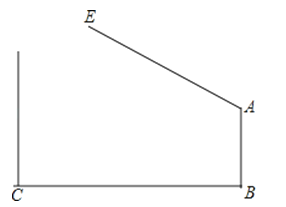
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com