练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，在平面直角坐标系xOy中，直线y=kx+$\frac{8}{5}$与经过原点O的抛物线y=ax2+bx+c交于点A（1，1）和点B（-4，m），与y轴交于点C
    （1）求抛物线的函数表达式；
    （2）设过点C的另一条直线与抛物线从左至右依次相交于E、F两点，若点E、F关于点C对称，求直线l的函数表达式和点E的坐标；
    （3）在（2）的条件下，连接OA、OB、OE、AE，在坐标平面内是否存在这样的点P，使得以B、O、P为顶点的△BOP与△OAE相似（其中，△BOP的顶点O与△OAE的顶点A是对应顶点）？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．

    分析 （1）根据待定系数法可求直线AB：y=-$\frac{3}{5}$x+$\frac{8}{5}$，将点B（-4，m）代入y=-$\frac{3}{5}$x+$\frac{8}{5}$可得B（-4，4），再根据待定系数法可求抛物线；
    （2）直线y=-$\frac{3}{5}$x+$\frac{8}{5}$，令x=0，可求C（0，$\frac{8}{5}$），设过点C的直线l解析式为y=k′x+$\frac{8}{5}$，联立$\left\{\begin{array}{l}{y=k′x+\frac{8}{5}}\\{y=\frac{2}{5}{x}^{2}+\frac{3}{5}x}\end{array}\right.$，消去y并整理得2x2+（3-5k′）x-8=0，根据点E、F关于点C对称，得到点C是线段EF的中点，得到$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{5k′-3}{4}$=0，可求直线l：y=$\frac{3}{5}$x+$\frac{8}{5}$，则2x2+（3-5×$\frac{3}{5}$）x-8=0，解得x=±2，进一步得到E（-2，$\frac{2}{5}$）；
    （3）如图所示，过点E作GH⊥AG于H，则AG=3，GH=1，EG=$\frac{3}{5}$，EH=$\frac{2}{5}$，OH=2，根据三角函数和三角形相似的判定和性质得到P点坐标，同理，点P关于直线OB：y=-x的对称点p′也符合题意，从而求解．

    解答 解：（1）将点A（1，1）代入直线y=kx+$\frac{8}{5}$得k+$\frac{8}{5}$=1，解得k=-$\frac{3}{5}$，
    则直线AB：y=-$\frac{3}{5}$x+$\frac{8}{5}$，
    将点B（-4，m）代入y=-$\frac{3}{5}$x+$\frac{8}{5}$得m=-$\frac{3}{5}$×（-4）+$\frac{8}{5}$，解得m=4，
    则B（-4，4），
    ∵抛物线y=ax2+bx+c经过点A，O，B，
    ∴$\left\{\begin{array}{l}{a+b+c=1}\\{16a-4b+c=4}\\{c=0}\end{array}\right.$，
    解得a=$\frac{2}{5}$，b=$\frac{3}{5}$，c=0．
    ∴抛物线的函数表达式为y=$\frac{2}{5}$x2+$\frac{3}{5}$x；
    （2）直线y=-$\frac{3}{5}$x+$\frac{8}{5}$，令x=0，解得y=$\frac{8}{5}$，
    则C（0，$\frac{8}{5}$），
    设过点C的直线l解析式为y=k′x+$\frac{8}{5}$，
    联立$\left\{\begin{array}{l}{y=k′x+\frac{8}{5}}\\{y=\frac{2}{5}{x}^{2}+\frac{3}{5}x}\end{array}\right.$，
    消去y并整理得2x2+（3-5k′）x-8=0，
    令E（x1，y1），F（x2，y2），则有x1+x2=$\frac{5k′-3}{2}$，
    ∵点E、F关于点C对称，
    ∴点C是线段EF的中点，
    ∴$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{5k′-3}{4}$=0，解得k′=$\frac{3}{5}$，
    ∴直线l：y=$\frac{3}{5}$x+$\frac{8}{5}$，
    ∴2x2+（3-5×$\frac{3}{5}$）x-8=0，
    解得x=±2，
    ∵E在F的左侧，
    ∴E（-2，$\frac{2}{5}$）；
    （3）OA=$\sqrt{2}$，OB=4$\sqrt{2}$，OE=$\frac{2\sqrt{26}}{5}$，AE=$\frac{3\sqrt{26}}{5}$，
    如图所示，过点E作GH⊥AG于H，则AG=3，GH=1，EG=$\frac{3}{5}$，EH=$\frac{2}{5}$，OH=2，
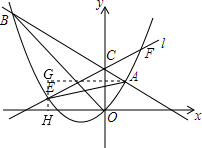    ∴tan∠EAG=$\frac{EG}{AG}$=$\frac{1}{5}$=$\frac{EH}{OH}$=tan∠EOH，
    ∴∠EAG=∠EOH，
    又∵∠OAG=∠BOH，
    ∴∠OAE=∠BOE，
    ∴存在点P，使得△BOP∽△OAE（O与A是对应点），
    则射线OE的解析式为：y=$\frac{1}{5}$x，
    ∴设P（m，$\frac{1}{5}$m）（m＜0），则OP=$\frac{\sqrt{26}}{5}$m，
    ∵△BOP∽△OAE（O与A是对应点），
    ∴$\frac{OP}{OB}$=$\frac{AE}{OA}$或$\frac{OP}{OB}$=$\frac{OA}{AE}$，即-$\frac{\frac{\sqrt{26}}{5}m}{4\sqrt{2}}$=$\frac{\frac{3\sqrt{26}}{5}}{\sqrt{2}}$或-$\frac{\frac{\sqrt{26}}{5}m}{4\sqrt{2}}$=$\frac{\sqrt{2}}{\frac{3\sqrt{26}}{5}}$，
    解得m1=-12，m2=-$\frac{100}{39}$，
    ∴p1（-12，$\frac{12}{5}$），p2（-$\frac{100}{39}$，$\frac{20}{39}$），
    同理，点p关于直线OB：y=-x的对称点p′也符合题意，
    ∴p3（-$\frac{12}{5}$，12），p4（-$\frac{20}{39}$，$\frac{100}{39}$）．

    点评 考查了二次函数综合题，解题的关键是熟练掌握待定系数法求直线的解析式，待定系数法求抛物线的解析式，对称的性质，三角函数，三角形相似的判定和性质等知识点，注意数形结合和方程思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．时钟的分针长5cm，经过15分钟，它的针尖转过的弧长是（　　）
    A．$\frac{25}{4}$πcmB．$\frac{15}{2}$πcmC．$\frac{5}{2}$πcmD．$\frac{5}{12}$πcm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知一次函数y=kx-4，函数值y随x的值增大而减小，那么k的取值范围是k＜0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知Rt△ABC，∠BAC=90°，将△ABC绕点C顺时针旋转得到△DEC（D与A是对应点），直线DA与直线BE交于点F．

    （1）求证：BF=EF；
    （2）如图2所示，点E落在射线CA上，连接CF交AB于点G，∠ABC的角平分线交CF于点H，P为BH上一点，且BH=4PH，直线AP交CF于点M，交BC于点N，若AF：AD=5：6，请你探究线段NP与MA之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：在△ABC中，∠C=90°，AC=BC，直线l绕点A旋转，过点B，C分别向直线l作垂线，垂足分别为点D，点E．
    （1）如图1，求证：BD+CE=AE；
    （2）当直线l绕点A顺时针旋转到如图2，则BD，CE，AE之间满足的数量关系是BD+AE=CE
    （3）在（2）的条件下，设CE与AB交于点P，若AP=$\sqrt{5}$，CP=5，连接BE，CD，线段CD分别与线段BP，线段BE相交于M，N两点（如图3），求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，在△ABC中，以AC边为直径的⊙O交BC于点D，过点B作BG⊥AC交⊙O于点E、H，连AD、ED、EC．若BD=8，DC=6，则CE的长为2$\sqrt{21}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．把两块全等的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，DF经过点B，其中∠ABC=∠DEF=90°，∠C=∠F=45°，AB=DE=4，把三角板ABC固定不动，让三角板DEF绕点O逆时针旋转，旋转角为α．其中0°＜α＜90°，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q．下面三个结论：
    （1）△APD∽△CDQ；
    （2）AP•CQ的值不变，为8；
    （3）当45°≤α＜90°时，设CQ=x，两块三角板重叠面积为$y=4-x-\frac{8-4x}{4-x}$．
    其中正确的是（　　）
    A．（1）与（2）B．（1）与（3）C．（2）与（3）D．全正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．若tanA=$\frac{\sqrt{2}}{4}$，则sinA的值是（　　）
    A．$\frac{4\sqrt{2}}{3}$B．$\frac{1}{3}$C．3D．$\frac{3\sqrt{2}}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．计算：cos30°•sin60°=$\frac{3}{4}$．

    查看答案和解析>>

    同步练习册答案