
如图,等圆⊙O1与⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,点A在x轴的正半轴上,两圆分别与x轴交于C、D两点,y轴与⊙O2相切于点O1,点O1在y轴的负半轴上.
①四边形AO1BO2为菱形;
②点D的横坐标是点O2的横坐标的两倍;
③∠ADB=60°;
④△BCD的外接圆的圆心是线段O1O2的中点.
以上结论正确的是 . (写出所有正确结论的序号)
(写出所有正确结论的序号)

①③.
【解析】
试题分析: ①连接AO1,AO2,BO1,BO2根据菱形的判定定理即可得出结论;
②根据垂径定理即可得出结论;
③连接O1O2,AB,BD,根据三角形中位线定理即可得出结论;
④先判断出△BCD是等边三角形,再根据等边三角形外心的性质即可得出结论.
试题解析:①如图1所示,连接AO1,AO2,B O1,BO2,
O1,BO2,
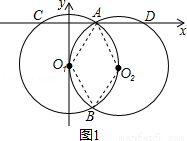
∵圆⊙O1与⊙O2是等圆,
∴AO1=AO2=BO1=BO2,
∴四边形AO1BO2为菱形,故此小题正确;
②∵AD是⊙O2的弦,
∴O2在线段AD的垂直平分线上,
∴点D的横坐标不是点O2的横坐标的两倍,故此小题错误;
③连接O1O2,AB,BD,
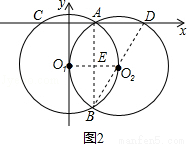
∵y轴是⊙O2的切线,
∴O1O2⊥y轴,
∵AD∥1O2.
∵四边形AO1BO2为菱形,
∴AB⊥O1O2,O1E=O2E,
∴∠BAD=90°,
∴BD过点O2,
∴O2E是△ABD的中位线,
∴AD=O1O2=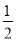 BD,
BD,
∴∠ADB=60°;
④∵由③知,2AD=BD,
∴CD=BD=BC,
∴△BCD的外心是各边线段垂直平分线的交点,
∵O1O2的中点是△BCD中位线的中点,
∴△BCD的外接圆的圆心不是线段O1O2的中点,故此小题错误.
考点:圆的综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(福建莆田卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( ,﹣2),反比例函数y=
,﹣2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:解答题
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)求证:直线 AB是⊙O的切线.
AB是⊙O的切线.
(2)若∠A=34°,AC=6,求⊙O的周长.(结果精确到0.01)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:选择题
下列说法正确的是( )
A.了解某班同学的身高情况适合用全面调查
B.数据2、3、4、2、3的众数是2
C.数据4、5、5、6、0的平均数是5
D.甲、乙两组数据的平均数相同,方差分别是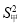 =3.2,
=3.2, =2.9,则甲组数据更稳定
=2.9,则甲组数据更稳定
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:填空题
如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:解答题
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
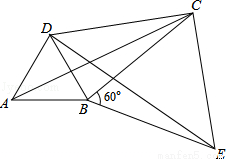
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com