
ИјГіЖЈвхЃЌШєвЛИіЫФБпаЮжаДцдкЯрСкСНБпЕФЦНЗНКЭЕШгквЛЬѕЖдНЧЯпЕФЦНЗНЃЌдђГЦИУЫФБпаЮЮЊЙДЙЩЫФБпаЮЃЎ
ЃЈ1ЃЉдкФубЇЙ§ЕФЬиЪтЫФБпаЮжаЃЌаДГіСНжжЙДЙЩЫФБпаЮЕФУћГЦЃЛ
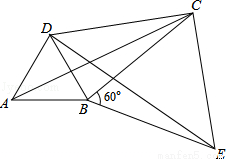
ЃЈ2ЃЉШчЭМЃЌНЋЁїABCШЦЖЅЕуBАДЫГЪБеыЗНЯђа§зЊ60ЁуЕУЕНЁїDBEЃЌСЌНгADЃЌDCЃЌCEЃЌвбжЊЁЯDCB=30ЁуЃЎ
ЂйЧѓжЄЃКЁїBCEЪЧЕШБпШ§НЧаЮЃЛ
ЂкЧѓжЄЃКDC2+BC2=AC2ЃЌМДЫФБпаЮABCDЪЧЙДЙЩЫФБпаЮЃЎ
(1)е§ЗНаЮЁЂОиаЮЁЂжБНЧЬнаЮОљПЩЃЛ
(2)ЂйжЄУїМћНтЮі
ЂкжЄУїМћНтЮі
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЙДЙЩЫФБпаЮЕФЖЈвхКЭЬиЪтЫФБпаЮЕФаджЪЃЌдђПЩЕУГіЃЛ
ЃЈ2ЃЉЂйгЩа§зЊЕФаджЪПЩжЊЁїABCЁеЁїDBEЃЌДгЖјПЩЕУBC=BEЃЌгЩЁЯCBE=60ЁуПЩЕУЁїBCEЮЊЕШБпШ§НЧаЮЃЛ
ЂкгЩЂйПЩЕУЁЯBCE=60ЁуЃЌДгЖјПЩжЊЁїDCEЪЧжБНЧШ§НЧаЮЃЌдйРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉе§ЗНаЮЁЂОиаЮЁЂжБНЧЬнаЮОљПЩЃЛ
ЃЈ2ЃЉЂйЁпЁїABCЁеЁїDBEЃЌ
ЁрBC=BEЃЌ
ЁпЁЯCBE=60ЁуЃЌ
ЁрЁїBCEЪЧЕШБпШ§НЧаЮЃЛ
ЂкгЩЂйЁїBCEЮЊЕШБпШ§НЧаЮЃЌ
ЁрBC=CEЃЌЁЯBCE=60ЁуЃЌ
ЁпЁЯDCB=30ЁуЃЌ
ЁрЁЯDCE=90ЁуЃЌ
дкRtЁїDCEжаЃЌ
DC2+CE2=DE2ЃЌ
ЁрDC2+BC2=AC2ЃЎ
ПМЕуЃК1ЁЂдФЖСЬтЃЛ2ЁЂа§зЊЕФаджЪЃЛ3ЁЂЕШБпШ§НЧаЮЕФХаЖЈгыаджЪЁЁ


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЃНЈФЯЦНОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌЕШдВЁбO1гыЁбO2ЯрНЛгкAЁЂBСНЕуЃЌЁбO1ОЙ§ЁбO2ЕФдВаФO2ЃЌЕуAдкxжсЕФе§АыжсЩЯЃЌСНдВЗжБ№гыxжсНЛгкCЁЂDСНЕуЃЌyжсгыЁбO2ЯрЧагкЕуO1ЃЌЕуO1дкyжсЕФИКАыжсЩЯЃЎ
ЂйЫФБпаЮAO1BO2ЮЊСтаЮЃЛ
ЂкЕуDЕФКсзјБъЪЧЕуO2ЕФКсзјБъЕФСНБЖЃЛ
ЂлЁЯADB=60ЁуЃЛ
ЂмЁїBCDЕФЭтНгдВЕФдВаФЪЧЯпЖЮO1O2ЕФжаЕуЃЎ
вдЩЯНсТле§ШЗЕФЪЧЁЁ ЁЁЃЎ ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЃНЈШ§УїОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ЯТСаМЦЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
AЃЎЃЈa3ЃЉ2=a5 BЃЎa6ЁТa3=a2 CЃЎЃЈabЃЉ2=a2b2 DЃЎЃЈa+bЃЉ2=a2+b2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЪЫрЬьЫЎОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
аДГівЛИіЭМЯѓОЙ§ЕуЃЈЉ1ЃЌ2ЃЉЕФвЛДЮКЏЪ§ЕФНтЮіЪНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЪЫрЬьЫЎОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
НЋЖўДЮКЏЪ§y=x2ЕФЭМЯѓЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ2ИіЕЅЮЛКѓЃЌЫљЕУЭМЯѓЕФКЏЪ§БэДяЪНЪЧЃЈЁЁЁЁЃЉ
AЃЎy=ЃЈxЉ1ЃЉ2+2 BЃЎy=ЃЈx+1ЃЉ2+2 CЃЎy=ЃЈxЉ1ЃЉ2Љ2 DЃЎy=ЃЈx+1ЃЉ2Љ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЪЫрРМжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ШчЭМЃЌдкЁїABCжаЃЌЯШзїЁЯBACЕФНЧЦНЗжЯпADНЛBCгкЕуDЃЌдйвдACБпЩЯЕФвЛЕуOЮЊдВаФЃЌЙ§AЁЂDСНЕузїЁбOЃЈгУГпЙцзїЭМЃЌВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЌВЂАбзїЭМКлМЃгУКкЩЋЧЉзжБЪМгКкЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈИЪЫрРМжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮOBCDЪЧБпГЄЮЊ4ЕФе§ЗНаЮЃЌЦНаагкЖдНЧЯпBDЕФжБЯпlДгOГіЗЂЃЌбиxжсе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдЫЖЏЕНжБЯпlгые§ЗНаЮУЛгаНЛЕуЮЊжЙЃЎЩшжБЯпlЩЈЙ§е§ЗНаЮOBCDЕФУцЛ§ЮЊSЃЌжБЯпlдЫЖЏЕФЪБМфЮЊtЃЈУыЃЉЃЌЯТСаФмЗДгГSгыtжЎМфКЏЪ§ЙиЯЕЕФЭМЯѓЪЧЃЈЁЁЁЁЃЉ





A B C D
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯГЄЩГОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
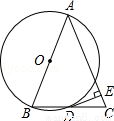
ШчЭМЃЌвдЁїABCЕФвЛБпABЮЊжБОЖзїЁбOЃЌЁбOгыBCБпЕФНЛЕуЧЁКУЮЊBCЕФжаЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛACгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЁЭACЃЛ
ЃЈ2ЃЉШєAB=3DEЃЌЧѓtanЁЯACBЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯГЛжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ИљОнЯрЙиВПУХЭГМЦЃЌ2014ФъЮвЙњЙВга9390000УћбЇЩњВЮМгИпПМЃЌ9390000гУПЦбЇМЧЪ§ЗЈБэЪОЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com