
A.m>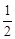 | B.m<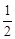 | C.m≥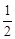 | D.m≤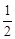 |
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:不详 题型:解答题
 、
、 分别表示一种白炽灯和一种节能灯的费用
分别表示一种白炽灯和一种节能灯的费用 (费用=灯的售价+电费,单位:元)与照明时间
(费用=灯的售价+电费,单位:元)与照明时间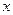 (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样。
(小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样。 、
、 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。| A.0 | B.1 | C.2 | D.大于2的整数 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.3 | B.2 | C.1 | D.0 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。
家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。 )已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
)已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
|

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.k>2 | B.k<2 | C.k>3 | D.k<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com