Question

【题目】如图，抛物线 （m＜0）的顶点为A，交y轴于点C．

（1）求出点A的坐标（用含m的式子表示）；
（2）平移直线y=x经过点A交抛物线C于另一点B，直线AB下方抛物线C上一点P，求点P到直线AB的最大距离
（3）设直线AC交x轴于点D，直线AC关于x轴对称的直线交抛物线C于E、F两点．若∠ECF=90°，求m的值．

Answer 1

【答案】
（1）

解：∵ ，

∴顶点A坐标

（2）

解：∵直线AB的解析式为 ，

设P ，

过点P作PQ∥y轴交AB于Q，如图1中，

∴Q

∴PQ=

= ，

当 时，PQ有最大值为 ，

∵PQ与直线AB的夹角为45°

∴P到直线AB的距离d的最大值为 ．

（3）

解：A（﹣m，﹣ m2+m）、C（0，m）

A′（﹣m， m2﹣m，）、C′（0，﹣m）

∴直线EF的解析式为y=﹣ mx﹣m，

设E（x1，y1）、F（x2，y2）

过点C作MN∥x轴，过点E作EM⊥MN于M，过点F作FN⊥MN于N，

∵∠ECF=90°，

∴∠ECM+∠FCN=90°，∠FCN+∠CFN=90°，

∴∠ECM=∠CFN，∵∠EMC=∠FNC=90°，

∴Rt△EMC∽Rt△CNF，∴ ，

即 ，

化简得：y1y2﹣m（y1+y2）+m2=﹣x1x2

由 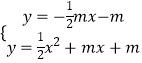，消去y，整理得：x2+3mx+4m=0

∴x1+x2=﹣3m，x1x2=4m

y1y2=（﹣ mx1﹣m）（﹣ mx2﹣m）=﹣ m3+m2

y1+y2= m2﹣2m，

∴﹣ m3+m2﹣m（ m2﹣2m）+m2=﹣4m，

∴m（m-2m-2）=0

解得m=1- 或1+ 或0，

∵m＜0，∴m=1- .

【解析】把抛物线的解析式写成顶点式的形式，表示出顶点；表示出PQ的距离，根据二次的函数的性质求最值。
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．