
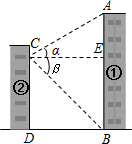
 某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)
某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)| BE |
| CE |
| AE |
| CE |
| AE |
| CE |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
| 3 |
| a |
| ab-b2 |
| b |
| a2-ab |
| a2+b2 |
| 2ab |
| 2 | ||
|
| 2 | ||
1-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
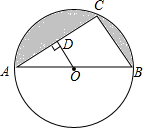 如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com