
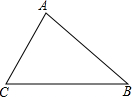
 在△ABC中,∠C>∠B,BC边上的高AD交BC于点D,∠BAC的角平分线AE交BC于点E.
在△ABC中,∠C>∠B,BC边上的高AD交BC于点D,∠BAC的角平分线AE交BC于点E.分析 (1)利用基本作图将图形补充完整;
(2)先根据三角形内角和定理计算出∠BAC=80°,再利用角平分线定义得到∠BAE=$\frac{1}{2}$∠BAC=40°,然后根据三角形外角性质可计算出∠CEA,再利用垂直定义和互余计算∠EAD的度数.
解答 解:(1)如图,AD、AE为所作;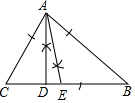
(2)∵∠B=40°,∠C=60°,
∴∠BAC=180°-40°-60°=80°,
∵AE是∠BAC的平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=40°,
∴∠CEA=∠B+∠BAE=80°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠EAD=90°-∠DEA=90°-80°=10°.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).


科目:初中数学 来源: 题型:选择题
| A. | 5.86% | B. | 5.88% | C. | 5.84% | D. | 5.82% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
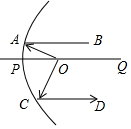 卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )| A. | 65° | B. | 75° | C. | 115° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
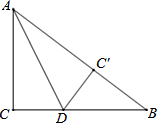 如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.
如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
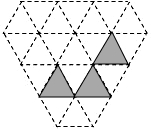 如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.
如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com