
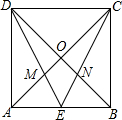
 已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.
已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$. 分析 利用面积转化S=r$•\frac{c}{2}$,由相似可得AM=$\frac{AC}{3}$,ME=$\frac{DE}{3}$,利用勾股定理可得AC,DE的长,从而得出四边形MENO的周长,由OM与OA的比例关系,易得△AOE的面积与△OME的面积比,可得△OME的面积,得四边形MENO的面积,根据周长与面积的关系得r.
解答 解:∵四边形ABCD为正方形,E为AB的中点,
∴AB∥CD,
∴△AME∽△CMD,
∵E为AB的中点,
∴$\frac{AE}{CD}=\frac{AM}{CM}=\frac{ME}{MD}$=$\frac{1}{2}$,
∴$\frac{AM}{AC}=\frac{1}{3}$,$\frac{ME}{DE}=\frac{1}{3}$,
∵AD=DC=1,
∴AE=$\frac{1}{2}$,
∴DE=$\frac{\sqrt{5}}{2}$,AC=$\sqrt{2}$,
∴ME=$\frac{\sqrt{5}}{6}$,AM=$\frac{\sqrt{2}}{3}$,
∴MO=AO-AM=$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{3}$=$\frac{\sqrt{2}}{6}$,
∴四边形MENO的周长为:2×($\frac{\sqrt{5}}{6}+\frac{\sqrt{2}}{6}$)=$\frac{\sqrt{5}+\sqrt{2}}{3}$,
∵S四边形MENO=2S△MEO,
∵$\frac{{S}_{△MEO}}{{S}_{△AEO}}$=$\frac{OM}{OA}$=$\frac{1}{3}$,S△AEO=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{8}$,
∴S△MEO=$\frac{1}{24}$,
∴S四边形MENO=$\frac{1}{12}$,
∴r=$\frac{1}{12}÷$($\frac{1}{2}$×$\frac{\sqrt{5}+\sqrt{2}}{3}$)=$\frac{\sqrt{5}-\sqrt{2}}{6}$,
故答案为:$\frac{\sqrt{5}-\sqrt{2}}{6}$.
点评 本题主要考查了多边形与其内切圆的关系,利用面积与周长的关系解得内切圆的半径是解答此题的关键.


科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图, 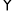 ABCD与
ABCD与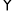 DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_________°.
DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_________°.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中复习数学检测试卷(一)(解析版) 题型:选择题
下列各式中与2mn﹣m2﹣n2相等的是( )
A.(m+n)2 B.﹣(m+n)2 C.(m﹣n)2 D.﹣(m﹣n)2
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
下列变形中,从左向右是因式分解的是( )
A. x2﹣9+6x=(x+3)(x﹣3)+6x B. x2﹣8x+16=(x﹣4)2
C. (x﹣1)2=x2﹣2x+1 D. x2+1=x(x+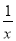 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
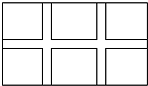 学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com