练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知△ABC为等边三角形，点D、E分别在边BC、AC上，且AE=CD，AD与BE相交于点F．则∠BFD的度数为（　　）

    A. 45° B. 90° C. 60° D. 30°

    【答案】C

    【解析】根据等边三角形性质得出AB=AC，∠BAE=∠C=60°，证△ABE≌△CAD，推出∠ABE=∠CAD，根据三角形外角性质求出∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC，即可求出答案．

    ∵△ABC是等边三角形，

    ∴AB=AC，∠BAE=∠C=60°，

    在△ABE和△CAD中，

    ∵AB=AC，

    ∠BAE=∠C，

    AE=CD，

    ∴△ABE≌△CAD(SAS)，

    ∴∠ABE=∠CAD，

    ∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

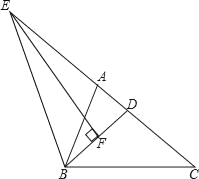
    【题目】在△ABC中，BD平分∠ABC，EF垂直平分BD交CA延长线于点E．

    （1）求证：ED2=EAEC；

    （2）若ED=6，BD=CD=3，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司今年销售一种产品，1月份获得利润20万元．由于产品畅销．利润逐月增加，3月份的利润比2月份的利润增加4.8万元，假设该产品利润每月的增长率相同，求这个增长率．设这个增长率为x

    （1）填空：（用含x的代数式表示）

    ①2月份的利润为：______

    ②3月份的利润为：______

    （2）列出方程，并求出问题的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，A F∥CE，且交BC于点F．

    （1）求证：△ABF≌△CDE；

    （2）如图，若∠1=65°，求∠B的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CE是圆O的直径，⊙O的直径，AB为⊙O的弦，EC⊥AB，垂足为D，下面结论正确的有（ ） ①AD=BD；② = ；③ = ；④OD=CD．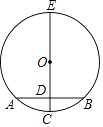

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣ x2+bx+c与x轴分别交于点A（﹣2，0）、B（4，0），与y轴交于点C．
    （1）求抛物线解析式；
    （2）求△CAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体，如图所示．

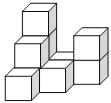
    （1）这个几何体由 个小正方体组成，请画出这个几何体的三视图；

    （2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 个正方体只有一个面是黄色，有 个正方体只有两个面是黄色，有 个正方体只有三个面是黄色；

    （3）若现在你手头还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方体．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线的不等式为y=﹣x2+6x+c．
    （1）若抛物线与x轴有交点，求c的取值范围；
    （2）设抛物线与x轴两个交点的横坐标分别为x1 ， x2 ． 若x12+x22=26，求c的值．
    （3）若P，Q是抛物线上位于第一象限的不同两点，PA，QB都垂直于x轴，垂足分别为A，B，且△OPA与△OQB全等．求证：c＞﹣ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

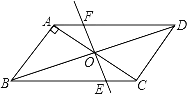
    【题目】如图，平行四边形ABCD中，AB⊥AC，AB=1，BC= ．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．

    （1）证明：当旋转角为90°时，四边形ABEF是平行四边形；

    （2）试说明在旋转过程中，线段AF与EC总保持相等；

    （3）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点O顺时针旋转的度数．

    查看答案和解析>>

    同步练习册答案