
【题目】如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 . 
【答案】![]() ≤CF≤3
≤CF≤3
【解析】解:∵四边形ABCD是矩形,
∴∠C=90°,BC=AD=5,CD=AB=3,
当点D与F重合时,CF最大=3,如图1所示: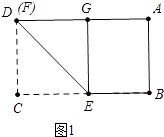
当B与E重合时,CF最小,如图2所示: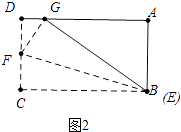
在RTABG中,∵BG=BC=5,AB=3,
∴AG= ![]() =4,
=4,
∴DG=AD﹣AG=1,设CF=FG=x,
在RT△DFG中,∵DF2+DG2=FG2 ,
∴(3﹣x)2+12=x2 ,
∴x= ![]() ,
,
∴ ![]() ≤CF≤3.
≤CF≤3.
故答案为 ![]() ≤CF≤3.
≤CF≤3.
当点E与B重合时,CF最小,先利用勾股定理求出AG,设CF=FG=x,在RT△DFG中,利用勾股定理列出方程即可解决问题,当F与D重合时,CF最大.由此即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(﹣6,1)B(﹣3,1)C(﹣3,3) 
(1)将Rt△ABC沿x轴正方向平移5个单位长度后得到Rt△A1B1C1 . 试在图中画出Rt△A1B1C1 , 并写出C1点的坐标;
(2)将Rt△ABC绕点B顺时针旋转90°后得到Rt△A2B2C2 . 试在图中画出Rt△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 和y=﹣
和y=﹣ ![]() 的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种服装,每件甲种服装比每件乙种服装贵25元,该商场用2000元购进甲种服装,用750元购进乙种服装,所购进的甲种服装的件数是所购进的乙种服装的件数的2倍.
(1)分别求每件甲种服装和每件乙种服装的进价;
(2)若每件甲种服装售价130元,将购进的两种服装全部售出后,使得所获利润不少于750元,问每件乙种服装售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,POOQ=y.
(1)①延长BC交ED于点M,则MD= , DC=;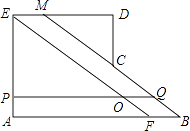
(2)求y关于x的函数解析式;
(3)当a≤x≤ ![]() (a>0)时,9a≤y≤6b,求a,b的值;
(a>0)时,9a≤y≤6b,求a,b的值;
(4)当1≤y≤3时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,O为BC的中点,AB与⊙O相切于点D. 
(1)求证:AC是⊙O的切线;
(2)若∠B=33°,⊙O的半径为1,求BD的长.(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).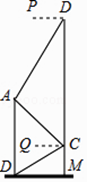
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com