
����Ŀ��ij�̳������ס������ַ�װ��ÿ�����ַ�װ��ÿ�����ַ�װ��25Ԫ�����̳���2000Ԫ�������ַ�װ����750Ԫ�������ַ�װ���������ļ��ַ�װ�ļ����������������ַ�װ�ļ�����2����
��1���ֱ���ÿ�����ַ�װ��ÿ�����ַ�װ�Ľ��ۣ�
��2����ÿ�����ַ�װ�ۼ�130Ԫ�������������ַ�װȫ���۳���ʹ��������������750Ԫ����ÿ�����ַ�װ�ۼ������Ƕ���Ԫ��
���𰸡�
��1���⣺���Ʒ�Ʒ�װÿ����ΪxԪ������Ʒ�Ʒ�װÿ����Ϊ��x��25��Ԫ��������ã�
![]() =
= ![]() ��2��
��2��
��ã�x=100��
�����飺x=100��ԭ��ʽ���̵Ľ⣬
x��25=100��25=75��
�𣺼ס�������Ʒ�Ʒ�װÿ���۷ֱ�Ϊ100Ԫ��75Ԫ
��2���⣺��ÿ�����ַ�װ�ۼ�������mԪ����������ã�
��130��100���� ![]() +��m��75����
+��m��75���� ![]() ��750��
��750��
��ã�m��90��
��ÿ�����ַ�װ�ۼ�������90Ԫ
����������1�����Ʒ�Ʒ�װÿ����ΪxԪ������Ʒ�Ʒ�װÿ����Ϊ��x��25��Ԫ�����ݹ����ļ��ַ�װ�ļ����������������ַ�װ�ļ�����2�����г����̣����x��ֵ�����ɵó��𰸣���2����ÿ�����ַ�װ�ۼ�������mԪ�����ݼ�һ����������ܵļ���+��һ����������ܵļ������������г�����ʽ�����m��ȡֵ��Χ�����ɵó��𰸣�
�����㾫����������Ŀ����֪���������÷�ʽ���̵�Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����з�ʽ���̽�Ӧ����IJ��裺���⡢��δ֪��������ȹ�ϵ�з��̡��ⷽ�̲������д���𰸣�Ҫ�е�λ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������
��1�����㣺|1�� ![]() |+��
|+�� ![]() ����1��2cos30�㣮
����1��2cos30�㣮
��2������ ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У���EΪAD���е㣬����BE����AC�ڵ�F����AF��CF=�� �� 
A.1��2
B.1��3
C.2��3
D.2��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��MΪ˫����y= ![]() �ϵ�һ�㣬����M��x�ᡢy��Ĵ��ߣ��ֱ�ֱ��y=��x+m�ڵ�D��C���㣬��ֱ��y=��x+m��y�ύ�ڵ�A����x���ཻ�ڵ�B��
�ϵ�һ�㣬����M��x�ᡢy��Ĵ��ߣ��ֱ�ֱ��y=��x+m�ڵ�D��C���㣬��ֱ��y=��x+m��y�ύ�ڵ�A����x���ཻ�ڵ�B��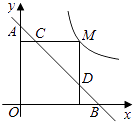
��1����ADBC��ֵ��
��2����ֱ��y=��x+mƽ�ƺ���˫����y= ![]() ����P��Q���㣬��PQ=3
����P��Q���㣬��PQ=3 ![]() ����ƽ�ƺ�m��ֵ��
����ƽ�ƺ�m��ֵ��
��3������M�ڵ�һ����˫�������˶�����˵����MPQ������Ƿ�������ֵ��������ڣ������������M�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E��F�ֱ���BC��DC�ϵ�һ�����㣬��EFΪ�Գ����۵���CEF��ʹ��C�ĶԳƵ�G����AD�ϣ���AB=3��BC=5����CF��ȡֵ��ΧΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮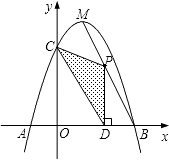
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��ΪԲ�ģ�����ͬ�ij�Ϊ�뾶�������ֱ�������AM��AN����B��C���㣬����BC���ٷֱ���B��CΪԲ�ģ�����ͬ�������� ![]() BC��Ϊ�뾶�����������ཻ�ڵ�D������AD��BD��CD�������н��۴�����ǣ� ��
BC��Ϊ�뾶�����������ཻ�ڵ�D������AD��BD��CD�������н��۴�����ǣ� �� 
A.ADƽ�֡�MAN
B.AD��ֱƽ��BC
C.��MBD=��NCD
D.�ı���ACDBһ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=a��x��1����x��4����x���ཻ�ڵ�A��B����A�ڵ�B����ࣩ����x���ཻ�ڵ�C����D���߶�CB�ϣ���D����B��C�غϣ�������D��CA��ƽ���ߣ����������ཻ�ڵ�E��ֱ��BC�Ľ���ʽΪy=kx+2��
��1�������ߵĽ���ʽΪ��
��2�����߶�DE�����ֵ��
��3������DΪBC���е�ʱ���ж��ı���CAED����״��������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com