
【题目】如图,抛物线y=a(x﹣1)(x﹣4)与x轴相交于点A、B(点A在点B的左侧),与x轴相交于点C,点D在线段CB上(点D不与B、C重合),过点D作CA的平行线,与抛物线相交于点E,直线BC的解析式为y=kx+2.
(1)抛物线的解析式为;
(2)求线段DE的最大值;
(3)当点D为BC的中点时,判断四边形CAED的形状,并加以证明.
【答案】
(1)y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
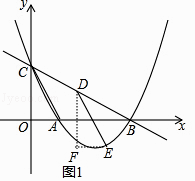
解:如图1,过点D、E分别作y轴、x轴的平行线,两线相交于点F,
当y=0时, ![]() (x﹣1)(x﹣4)=0,解得x1=1,x2=4,则A(1,0),B(4,0),
(x﹣1)(x﹣4)=0,解得x1=1,x2=4,则A(1,0),B(4,0),
设直线BC的解析式为y=kx+b,
把C(0,2),B(4,0)代入得 ![]() ,解得
,解得 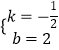 ,
,
∴直线BC的解析式为y=﹣ ![]() x+2,
x+2,
设E(m, ![]() m2﹣
m2﹣ ![]() m+2),EF=n,则D(m﹣n,﹣
m+2),EF=n,则D(m﹣n,﹣ ![]() m+
m+ ![]() n+2),
n+2),
∴DF=﹣ ![]() m+
m+ ![]() n+2﹣(
n+2﹣( ![]() m2﹣
m2﹣ ![]() m+2)=﹣
m+2)=﹣ ![]() m2+2m+
m2+2m+ ![]() n,
n,
∵OC∥DF,
∴∠OCB=∠FDB,
∵DE∥CA,
∴∠ACB=∠EDB,
∴∠OCA=∠FDE,
∴Rt△OCA∽Rt△FDE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴﹣ ![]() m2+2m+
m2+2m+ ![]() n=2n,
n=2n,
∴n=﹣ ![]() m2+
m2+ ![]() m,
m,
在Rt△DEF中,DE= ![]() =
= ![]() EF=
EF= ![]() n=﹣
n=﹣ ![]() m2+
m2+ ![]() m,
m,
∵DE=﹣ ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,
,
∴当m=2时,DE的长有最大值,最大值为 ![]() ;
;
(3)
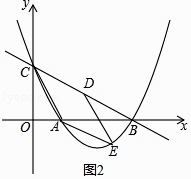
解:四边形CAED为菱形.理由如下:
AC= ![]() =
= ![]() ,BC=
,BC= ![]() =2
=2 ![]() ,
,
∵点D为BC的中点,
∴D(2,1),CD= ![]() ,
,
易得直线AC的解析式为y=﹣2x+2,
设直线DE的解析式为y=﹣2x+p,
把D(2,1)代入得1=﹣4+p,解得p=4,
∴直线DE的解析式为y=﹣2x+5,
解方程组 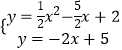 得
得 ![]() 或
或 ![]() ,则E(3,﹣1),
,则E(3,﹣1),
∴DE= ![]() =
= ![]() ,
,
∴AC=DE,
而AC∥DE,
∴四边形CAED为平行四边形,
∵CA=CD,
∴四边形CAED为菱形.
【解析】解:(1)当x=0时,y=kx+2=2,则C(0,2),
把C(0,2)代入y=a(x﹣1)(x﹣4)得a(﹣1)(﹣4)=2,解得a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣1)(x﹣4),即y=
(x﹣1)(x﹣4),即y= ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
所以答案是y= ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种服装,每件甲种服装比每件乙种服装贵25元,该商场用2000元购进甲种服装,用750元购进乙种服装,所购进的甲种服装的件数是所购进的乙种服装的件数的2倍.
(1)分别求每件甲种服装和每件乙种服装的进价;
(2)若每件甲种服装售价130元,将购进的两种服装全部售出后,使得所获利润不少于750元,问每件乙种服装售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若 ![]() 的长为
的长为 ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上 的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分. 
分组 | 次数x(个) | 人数 |
A | 0≤x<120 | 24 |
B | 120≤x<130 | 72 |
C | 130≤x<140 | |
D | x≥140 |
根据以上信息,解答下列问题:
(1)在被调查的学生中,跳绳次数在120≤x<130范围内的人数为人,跳绳次数在0≤x<120范围内的人数占被调查人数的百分比为%;
(2)本次共调查了名学生,其中跳绳次数在130≤x<140范围内的人数为人,跳绳次数在x≥140范围内的人数占被调查人数的百分比为%;
(3)该区七年级共有4000名学生,估计该区七年级学生1分钟跳绳的次数不少于130个的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).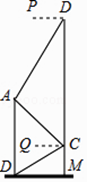
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在反比例函数y= ![]() (x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD=
(x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD= ![]() AB,延长BA到点E,使AE=
AB,延长BA到点E,使AE= ![]() AC,直线DE分别交x、y轴于点P、Q,当
AC,直线DE分别交x、y轴于点P、Q,当 ![]() =
= ![]() 时,则△ACE与△ADB面积之和等于 .
时,则△ACE与△ADB面积之和等于 . 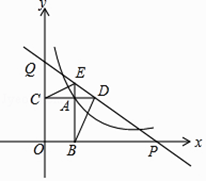
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣5,0)、C(﹣1,0),P(a,b)是△ABC的边AC上一点:
(1)将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 ![]() .
.
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com