
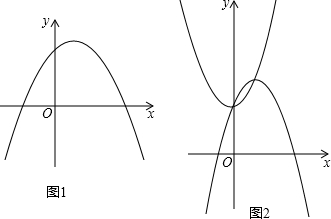
���� ��1��������ʽ��ɶ���ʽ���ɣ�
��2��ֱ��y=kx-k�����㣨1��0��������ʾ��ͼ�����A��B�������꣮����ֱ��y=kx-k�����㣨1��0�������PCD���PDC����������ֱ�ǣ����ԡ�CPDҪΪֱ�������Σ�ֻ�С�CPD=90��һ���������AP��BP��������һ����ļ��ι�ϵ�����ɹ��ɶ�������AP��BPб��֮��Ϊ-1�г����̣���֮���ɣ����ڲ�֪��б��֮��Ϊ-1��ͬѧ��ͨ�����������������������ƱȽ������������һ���ģ�
��3�����M��N�������꣬����Q��MN�е㣬��Q����������M��N�������ʾ�����ɱ�ʾ��Q��켣���̣����ڸ�����������C2Ҳ����P����P���������ɵ�a+c=0����һ��ϵʽʹ��Q�켣����ʽ�еIJ���a��c�������ȥ�ˣ��Ӷ��ó�Q��켣���̣�
��� �⣺��1����y=ax2-2ax+a+4=a��x-1��2+4��
�ú���ͼ�����һ�����ڵĶ���P��
���P�������ǣ�1��4����
��2����y=kx-k=k��x-1����
��ֱ��y=kx-k�����㣨1��0����
��ͼ1����A��x1��y1����B��x2��y2����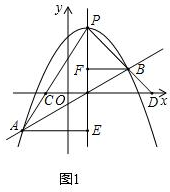
���������飺$\left\{\begin{array}{l}{y=kx-k}\\{y=a{x}^{2}-2ax+a+4}\end{array}\right.$��
��ȥy�����ã�ax2-��2a+k��x+��a+k+4��=0��
��Τ�ﶨ����֪��$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2+\frac{k}{a}}\\{{x}_{1}•{x}_{2}=1+\frac{k}{a}+\frac{4}{a}}\end{array}\right.$��
�Ӷ��ɵã�$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{{k}^{2}}{a}}\\{{y}_{1}•{y}_{2}=\frac{4{k}^{2}}{a}}\end{array}\right.$��
����A��AE�ͶԳ����ڵ�E������B��BF�ͶԳ����ڵ�F��
�ߡ�CPD��ֱ�������Σ���AP��BP��
���AEP�ס�PFB��
��$\frac{PE}{AE}=\frac{BF}{PF}$������$\frac{4-{y}_{1}}{1-{x}_{1}}=\frac{{x}_{2}-1}{4-{y}_{2}}$��
��16-4��y1+y2��+y1•y2=-x1•x2+��x1+x2��-1��
��16-4•$\frac{{k}^{2}}{a}$+$\frac{4{k}^{2}}{a}$=-1-$\frac{k}{a}$-$\frac{4}{a}$+2+$\frac{k}{a}$-1��
��a=-$\frac{1}{4}$��
��3����������C2���㣨1��4����
��c+1+2a+3+c=4��
��a+c=0��
��M��m����c+1��m2+��2a+3��m+c������N��m��am2-2am+a+4����Q��x��y��
��QΪMN�е㣬
��$\left\{\begin{array}{l}{x=m}\\{y=\frac{��c+1��{m}^{2}+��2a+3��m+c+a{m}^{2}-2am+a+4}{2}}\end{array}\right.$
��y=$\frac{��a+c+1��{x}^{2}+3x+a+c+4}{2}$=$\frac{1}{2}{x}^{2}+\frac{3}{2}x+2$��
���� ���⿼�������߹�������ж���ֱ���������ߵ�λ�ù�ϵ��Τ�ﶨ����Ӧ�á�ֱ�������ε����ʡ����������ε��ж������ʡ��켣���̵��ȶ��֪ʶ�㣬�ۺ��Ժͼ����Ժ�ǿ���ڣ�2���ʵĹؼ���������ֱ�������ε��ص㹹�������������г��߶α������̣��ڣ�3���ʱ����ѶȲ����ò�����ʾ��M��N��Q�����꣬��ȥ�������ǹ켣���̣�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ˰��% |
| ����3500Ԫ��������5000Ԫ�IJ��� | 3 |
| ����5000Ԫ��������8000Ԫ�IJ��� | 10 |
| ����8000Ԫ��������12500Ԫ�IJ��� | 20 |
| ����12500Ԫ��������38500Ԫ�IJ��� | 25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
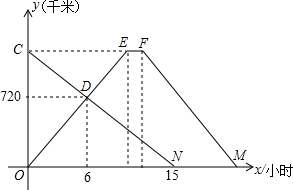 �쳵�������ҷֱ��A��B��վͬʱ������������У��쳵����Bվ��ͣ��1Сʱ��Ȼ��ԭ·ԭ�ٷ���Aվ����������Aվ��ͣ����Ϣ����ͼ��ʾ����������Aվ�ľ���y��ǧ�ף�����ʻʱ��x��Сʱ���ĺ���ͼ������ͼ����Ϣ������������⣺
�쳵�������ҷֱ��A��B��վͬʱ������������У��쳵����Bվ��ͣ��1Сʱ��Ȼ��ԭ·ԭ�ٷ���Aվ����������Aվ��ͣ����Ϣ����ͼ��ʾ����������Aվ�ľ���y��ǧ�ף�����ʻʱ��x��Сʱ���ĺ���ͼ������ͼ����Ϣ������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
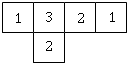 ��ͼ���ɼ���С�������������ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ������뻭����������������ͼ������ͼ��
��ͼ���ɼ���С�������������ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ������뻭����������������ͼ������ͼ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com