
分析 (1)利用M在第三象限及象限性质,列出关于a的不等式组,解不等式组求出A的取值范围,利用整点性质确定a的值,进而求出点M的坐标;
(2)根据点M的坐标,求出线段OH、MH长度,利用面积公式求出面积即可.
解答 解:(1)∵点M(2a-5,3-2a)是平面直角坐标系第三象限内的整点,
∴$\left\{\begin{array}{l}{2a-5<0}\\{3-2a<0}\end{array}\right.$,且a为$\frac{1}{2}$的整数倍,
解得:$\frac{3}{2}$<a<$\frac{5}{2}$,
∵a为$\frac{1}{2}$的整数倍,
∴a=2,
∴2a-5=-1,3-2a=-1,
∴M的坐标为(-1,-1).
(2)∵M(-1,-1),MH⊥x轴,
∴MH=1,OM=1,
∴S△OMH=$\frac{1}{2}$×OH×MH,
=$\frac{1}{2}$×1×1,
=$\frac{1}{2}$.
答:三角形OMH的面积为$\frac{1}{2}$.
点评 题目考查了平面直角坐标系与图形的性质及求直角三角形面积等知识点,学生需要识记每个象限点的特征及熟练解决不等式组的运算,题目整体较为简单.


科目:初中数学 来源: 题型:选择题
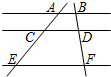 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AC}{AE}$=$\frac{CD}{EF}$ | B. | $\frac{AC}{BD}$=$\frac{CE}{DF}$ | C. | $\frac{AC}{CE}$=$\frac{AB}{CD}$ | D. | $\frac{AC}{DF}$=$\frac{BD}{CE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
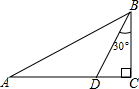 如图所示,在△ABC中,∠C=90°,AB=4$\sqrt{3}$.点D在边AC上,且AD=BD,∠DBC=30°.求:
如图所示,在△ABC中,∠C=90°,AB=4$\sqrt{3}$.点D在边AC上,且AD=BD,∠DBC=30°.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
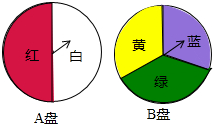 小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
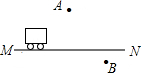 如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.
如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
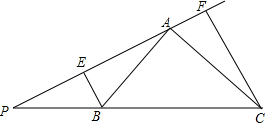 如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com