
 如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.分析 (1)由于反比例函数的值小于一次函数的值,故反比例函数需要在一次函数的图象的下方,根据图象即可求出x的范围;
(2)过点A作AC⊥AB交双曲线于点C,交y轴于点D,过点A作AE⊥y轴于点E,根据条件求出直线AC的解析式,然后联立直线AC与双曲线即可求出点C的坐标
解答 解:(1)由$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{3}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$
解得A(1,3),B(-3,-1)
当反比例函数的值小于一次函数的值-3<x<0或x>1;
(2)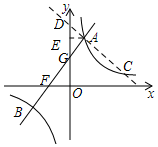 过点A作AC⊥AB交双曲线于点C,交y轴于点D,
过点A作AC⊥AB交双曲线于点C,交y轴于点D,
过点A作AE⊥y轴于点E,
令x=0代入y=x+2,
∴y=2,
∴G(0,2)
令y=0代入y=x+2,
∴x=-2,
∴F(-2,0)
∴OF=OG
∴∠GFO=45°,
∴∠AGE=45°,
∴△DAG是等腰直角三角形,
∵A(1,3)
∴OE=3,AE=1,
∴AE=DE=1,
∴OD=OE+DE=4,
∴D(0,4)
设直线AC的解析式为y=mx+n,
把(0,4)和(1,3)代入y=mx+n
∴$\left\{\begin{array}{l}{4=n}\\{3=m+n}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-1}\\{n=4}\end{array}\right.$
∴y=-x+4,
联立$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{3}{x}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$
∴点C(3,1).
点评 本题考查反比例函数的综合问题,解题的关键是联立两函数的解析式求出交点坐标,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 实数a,b在数轴上的位置如图,化简$\sqrt{(a-b)^{2}}$-$\frac{a(a+b)}{|a+b|}$的结果为( )
实数a,b在数轴上的位置如图,化简$\sqrt{(a-b)^{2}}$-$\frac{a(a+b)}{|a+b|}$的结果为( )| A. | b | B. | -b | C. | -2a+b | D. | 2a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )
如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )| A. | 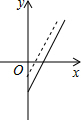 | B. | 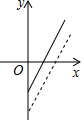 | C. | 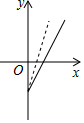 | D. | 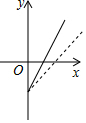 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com