
【题目】如图,△ABC中AB=AC , ∠C=30°,AB的垂直平分线MN分别交BC、AB于点M、N , 试探究BM与CM之间的数量关系. 
【答案】解:连接AM , ∵AB=BC , ∠C=30°, ∴∠B=30°,∵AB的垂直平分线是MN,∴∠MAC=90°,CM=2AM,∴AB=2BM,∴CM=2BM,
【解析】连接AM,∵AB=BC , ∠C=30°∴∠B=30°, ∵AB的垂直平分线是MN,,∴∠MAC=90°,CM=2AM, ∴AB=2BM,,∴CM=2BM.
【考点精析】通过灵活运用线段垂直平分线的性质和等腰三角形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.(结果精确到0.01m,已知![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中的顶点A、C分别在平面直角坐标系的x轴、y轴上,且∠ACB=90°,AC=2,BC=1,当点A从原点出发朝x轴的正方向运动,点C也随之在y轴上运动,当点C运动到原点时点A停止运动,连结OB.
(1)点A在原点时,求OB的长;
(2)当OA=OC时,求OB的长;
(3)在整个运动过程中,OB是否存在最大值?若存在,请你求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
特例探索
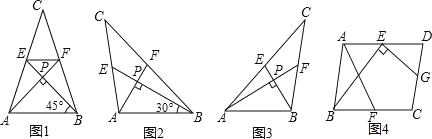
(1)如图1,当∠ABE=45°,c=2![]() 时,a=_____________,b=_____________.
时,a=_____________,b=_____________.
如图2,当∠ABE=30°,c=4时,a=_____________,b=_____________.
归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com