
 已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.| DE |
| OP |
| BD |
| BP |
| OB2-OP2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
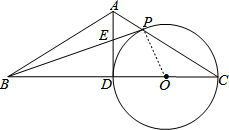 (1)证明:∵AB=AC,点D是边BC的中点,
(1)证明:∵AB=AC,点D是边BC的中点,| DE |
| OP |
| BD |
| BP |
| OB2-OP2 |
| 32-12 |
| 2 |
| 1×2 | ||
2
|
| ||
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
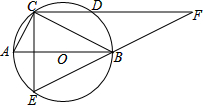 如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=
如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
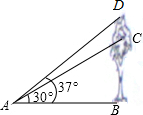 九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)
九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
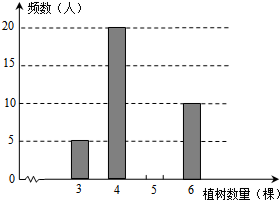 今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).| 植树数量(棵) | 频数 | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | |
| 5 | 0.3 | |
| 6 | 10 | 0.2 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
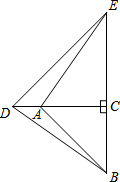 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.
如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积.若关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为
如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积.若关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为查看答案和解析>>
科目:初中数学 来源: 题型:
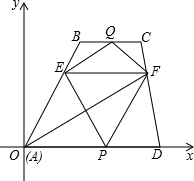 如图,在梯形ABCD中,BC∥AD,EF∥BC交AB于E,CD于F,P、Q分别为边AD和BC上的动点.若∠FAD=30°,AF=4
如图,在梯形ABCD中,BC∥AD,EF∥BC交AB于E,CD于F,P、Q分别为边AD和BC上的动点.若∠FAD=30°,AF=4| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com