
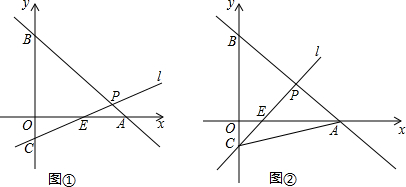
分析 (1)过点P作PD⊥y轴于D,根据等腰三角形三线合一的性质求得BD=DC=4O,进而求得OD=OC=2,然后根据平行线分线段成比例定理即可求得PD,即可求得P的坐标,然后根据$\frac{OE}{PD}$=$\frac{OC}{CD}$,求得OE的长度,从而求得E的坐标.
(2)先求出E点的坐标,就可以求出直线AB、PC的解析式.求出两条直线的交点P,再根据S△PAC=S△PAE+S△CAE就可以求解.
解答 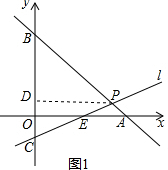 解:(1)如图1,过点P作PD⊥y轴于D,
解:(1)如图1,过点P作PD⊥y轴于D,
∵B(0,6),C(0,-2),
∴BC=8,
∵PB=PC,
∴BD=DC=4.
∵OB=6,
∴OD=2,OC=2,
∵PD∥OA,
∴$\frac{PD}{OA}$=$\frac{BD}{OB}$
即$\frac{PD}{8}$=$\frac{4}{6}$,
∴PD=$\frac{16}{3}$,
∴P($\frac{16}{3}$,2),
∵PD∥OA,
∴$\frac{OE}{PD}$=$\frac{OC}{CD}$,
即$\frac{OE}{\frac{16}{3}}$=$\frac{2}{4}$,
∴OE=$\frac{8}{3}$,
∴E($\frac{8}{3}$,0);
(2)如图2,∵$\frac{OC}{OE}$=$\frac{5}{4}$,OC=2,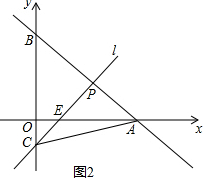
∴OE=$\frac{8}{5}$,
∴E($\frac{8}{5}$,0),
∴OE=8-$\frac{8}{5}$=$\frac{32}{5}$,
由题意可设直线PC的解析式为y=kx-2,
∵直线l经过E($\frac{8}{5}$,0),
∴$\frac{8}{5}$k-2=0,
∴k=$\frac{5}{4}$.
∴直线l的解析式为y=$\frac{5}{4}$x-2.
∵A(8,0),B(0,6),
∴直线AB的解析式为y=-$\frac{3}{4}$x+6.
解$\left\{\begin{array}{l}{y=-\frac{3}{4}x+6}\\{y=\frac{5}{4}x-2}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$.
∴P(4,3).
S△PAC=S△PAE+S△CAE=$\frac{1}{2}$×$\frac{32}{5}$×3+$\frac{1}{2}$×$\frac{32}{5}$×2=16.
点评 本题主要考查了平行线分线段成比例定理,待定系数法求函数解析式,并且考查不规则图形的面积可以转化为求一些规则图形或易求面积的图形的和或差的计算.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
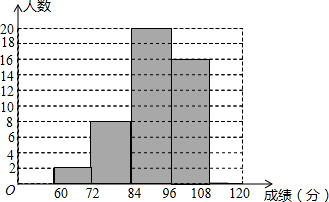 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题. | 频数 | 频率 | |
| 60<x≤72 | 2 | 0.04 |
| 72<x≤84 | 8 | 0.16 |
| 84<x≤96 | 20 | a |
| 96<x≤108 | 16 | 0.32 |
| 108<x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (-1,-3) | C. | (-3,1) | D. | (-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 |
| 电表显示(度) | 117 | 120 | 124 | 129 | 135 | 138 | 142 | 145 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com