
【题目】如图,二次函数![]() 的图象过原点,与x轴的另一个交点为
的图象过原点,与x轴的另一个交点为![]()
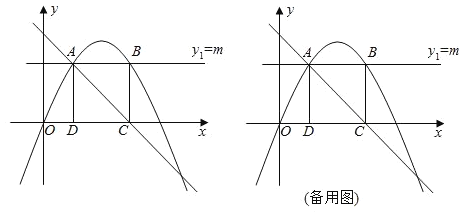
(1)求该二次函数的解析式;
(2)在x轴上方作x轴的平行线![]() ,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;
,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;
(3)在(2)的条件下,动点P从点A出发沿射线AB以每秒1个单位长度匀速运动,同时动点Q以相同的速度从点A出发沿线段AD匀速运动,到达点D时立即原速返回,当动点Q返回到点A时,P、Q两点同时停止运动,设运动时间为t秒(![]() ).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.
).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.
【答案】(1)![]() ;(2)当矩形ABCD为正方形时,m的值为4;(3)以A、E、F、Q四点为顶点构成的四边形能为平行四边形,t的值为4或6.
;(2)当矩形ABCD为正方形时,m的值为4;(3)以A、E、F、Q四点为顶点构成的四边形能为平行四边形,t的值为4或6.
【解析】
(1)根据点的坐标,利用待定系数法即可求出二次函数的解析式;
(2)利用二次函数图象上点的坐标特征求出点A,B的坐标,进而可得出点C,D的坐标,再利用正方形的性质可得出关于m的方程,解之即可得出结论;
(3)由(2)可得出点A,B,C,D的坐标,根据点A,C的坐标,利用待定系数法可求出直线AC的解析式,利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征可求出点E,F的坐标,由![]() 且以A、E、F、Q四点为顶点的四边形为平行四边形可得出
且以A、E、F、Q四点为顶点的四边形为平行四边形可得出![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况找出AQ,EF的长,由
三种情况找出AQ,EF的长,由![]() 可得出关于t的一元二次方程,解之取其合适的值即可得出结论.
可得出关于t的一元二次方程,解之取其合适的值即可得出结论.
(1)将![]() ,
,![]() 代入
代入![]() ,得:
,得: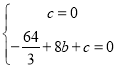 ,
,
解得![]() ,
,
∴该二次函数的解析式为![]() .
.
(2)当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
∴点a的坐标为(![]() ,m),点b的坐标为(
,m),点b的坐标为(![]() ,m),
,m),
∴点d的坐标为(![]() ,0),点c的坐标为(
,0),点c的坐标为(![]() ,0).
,0).
∵矩形abcd为正方形,
∴![]() ,
,
解得:![]() ,(舍去),
,(舍去),![]() .
.
∴当矩形ABCD为正方形时,m的值为4.
(3)以A、E、F、Q四点为顶点构成的四边形能为平行四边形.
由(2)可知:点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.
设直线AC的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴直线ac的解析式为![]() .
.
当![]() 时,
时,![]() ,
,![]()
∴点E的坐标为(![]() ,
,![]() ),点F的坐标为(
),点F的坐标为(![]() ,
,![]() -t+4).
-t+4).
∵以A、E、F、Q四点为顶点构成的四边形为平行四边形,且![]() ,
,
∴![]() ,分三种情况考虑:
,分三种情况考虑:
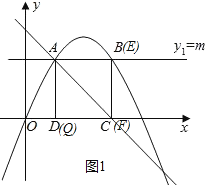
①当![]() 时,如图1所示,
时,如图1所示,![]() ,EF=
,EF=![]() ,
,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ;
;
②当![]() 时,如图2所示,
时,如图2所示,![]() ,EF=
,EF=![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ;
;
![]() ,
,![]() , EF=
, EF=![]() ,
,
![]() ,
,
解得![]() (舍去),
(舍去),![]() (舍去)
(舍去)
综上所述,当以A、E、F、Q四点为顶点构成的四边形为平行四边形时,t的值为4或6


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
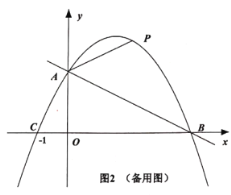
【题目】如图,一次函数![]() 的图像与坐标轴交于A、B两点,点C的坐标为
的图像与坐标轴交于A、B两点,点C的坐标为![]() ,二次函数
,二次函数![]() 的图像经过A、B、C三点.
的图像经过A、B、C三点.
(1)求二次函数的解析式
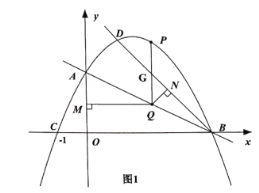
(2)如图1,已知点![]() 在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作
在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作![]() 轴于点M,作
轴于点M,作![]() 于点N,过Q作
于点N,过Q作![]() 轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足![]() ,求点E的坐标.
,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
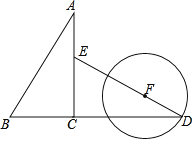
【题目】如图,Rt△ABC中,∠ACB=90°,BC=3,tanA=![]() ,将Rt△ABC绕点C顺时针旋转90°得到△DEC,点F是DE上一动点,以点F为圆心,FD为半径作⊙F,当FD=_____时,⊙F与Rt△ABC的边相切.
,将Rt△ABC绕点C顺时针旋转90°得到△DEC,点F是DE上一动点,以点F为圆心,FD为半径作⊙F,当FD=_____时,⊙F与Rt△ABC的边相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不超过160元/件,且每年售价确定以后不再变化,该产品的年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求2017年该公司的最大利润?
(3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元.若能,求出2018年产品的售价;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
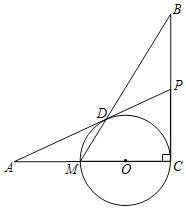
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店在开学初用880元购进若干个学生专用科学计算器,按每个50元出售,很快就销售一空,据了解学生还急需3倍这种计算器,于是又用2580元购进所需计算器,由于量大每个进价比上次优惠1元,该店仍按每个50元销售,最后剩下4个按九折卖出.这笔生意该店共盈利( )元.
A.508 B.520 C.528 D.560
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com