
����Ŀ���˳����ѾƲ���ɽ��ԫ��.������Զ�ں������������̳��Ϊ��������������ϲ����������Ϊ������������.���Ѿ����г�������������ݼ۸�ı仯���仯.���Ѿ�ÿƿ�ijɱ�����![]() Ԫ��ij���н��ۼ۶�Ϊ
Ԫ��ij���н��ۼ۶�Ϊ![]() Ԫʱ��ÿ���������
Ԫʱ��ÿ���������![]() ƿ�����ۼ�ÿ����
ƿ�����ۼ�ÿ����![]() Ԫ��ÿ�켴�ɶ�����
Ԫ��ÿ�켴�ɶ�����![]() ƿ(�ۼ۲��ܸ���
ƿ(�ۼ۲��ܸ���![]() Ԫ)������ÿƿ����
Ԫ)������ÿƿ����![]() Ԫ
Ԫ
![]() �ú�
�ú�![]() �Ĵ���ʽ��ʾ���Ѿ�ÿ���������.
�Ĵ���ʽ��ʾ���Ѿ�ÿ���������.
![]() ÿƿ���ѾƵ��ۼ۶�Ϊ����Ԫʱÿ���ȡ�����������������Ƕ��٣�
ÿƿ���ѾƵ��ۼ۶�Ϊ����Ԫʱÿ���ȡ�����������������Ƕ��٣�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����Ϊ����2![]() ��0������OAB=90������AOB=30��������OAB�Ƶ�O��˳ʱ�뷽����ת����ת��Ϊ����0��������150����������ת�����У���A��B�Ķ�Ӧ��ֱ�Ϊ��A����B����
��0������OAB=90������AOB=30��������OAB�Ƶ�O��˳ʱ�뷽����ת����ת��Ϊ����0��������150����������ת�����У���A��B�Ķ�Ӧ��ֱ�Ϊ��A����B����
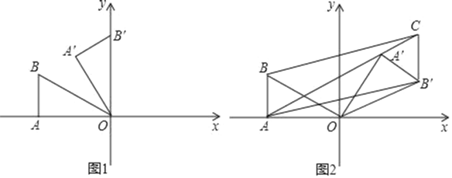
��1����ͼ1������=60��ʱ��ֱ��д����A���� ����B���� �������ꣻ
��2����ͼ2������=135��ʱ������B����AB��ƽ���߽�AA���ӳ����ڵ�C������BC��AB����
���ж��ı���AB��CB����״����˵�����ɣ�
�����ʱ��A���͵�B�������ꣻ
��3��������30����ת��150��ʱ����2���е��߶�B��CҲ��֮�ƶ��������B��C��ɨ����������������ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
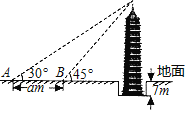
����Ŀ�������б������Ե����ٱ���ʼ�������ξ���䣬�ܱ߷羰���������������ڵ���Լ7�ף�ijУѧ����ù���������߶�ԼΪ40�ף������������Ե���߶ȵĹ������£����ڵ���A���������������Ϊ30����������������н�a��B������B���������������Ϊ45������ͼ��ʾ������ôa��ֵԼΪ_____�ף�![]() ��1.73�������ȷ��0.1����
��1.73�������ȷ��0.1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��0��4����B��6��0����������������y=![]() ��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��1������������ֱ��EF�Ľ���ʽ��
��2������OEF�������
��3������ͼ��ֱ��д������ʽk2x+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ������A��![]() ��0����B��0��2�������B2018������Ϊ��������
��0����B��0��2�������B2018��������������

A. ��6048��0��B. ��6054��0��C. ��6048��2��D. ��6054��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���yx3��ͼ���뷴��������y![]() (kΪ��������k0)��ͼ����A��1��a����B���㣮
(kΪ��������k0)��ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
������![]() ��
��![]() ����ͼ��
����ͼ��![]() ������
������![]() ��4��1����ֱ��
��4��1����ֱ��![]() ��ͼ��
��ͼ��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2���ᡢ�����궼�������ĵ�������㣮��ͼ��![]() �ڵ�
�ڵ�![]() ��
��![]() ֮��IJ������߶�
֮��IJ������߶�![]() ��
��![]() ��
��![]() Χ�ɵ��������߽磩Ϊ
Χ�ɵ��������߽磩Ϊ![]() ��
��
�ٵ�![]() ʱ��ֱ��д������
ʱ��ֱ��д������![]() �ڵ����������
�ڵ����������
��������![]() ��ǡ��4�����㣬��Ϻ���ͼ����
��ǡ��4�����㣬��Ϻ���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
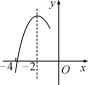
����Ŀ����ͼ��������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x����2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b��0����c<0���ۣ�3a��c>0����4a��2b>at2��bt��tΪʵ�������ݵ�![]() ��
��![]() ��
��![]() �Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
�Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com