
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

【答案】(1)反比例函数解析式为y=![]() ;直线EF的解析式为y=﹣
;直线EF的解析式为y=﹣![]() x+5;(2)
x+5;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)先利用矩形的性质确定C点坐标(6,4),再确定A点坐标为(3,2),则根据反比例函数图象上点的坐标特征得到k1=6,即反比例函数解析式为y=![]() ;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(
;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(![]() ,4),再利用待定系数法求直线EF的解析式;
,4),再利用待定系数法求直线EF的解析式;
(2)利用△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF进行计算;
(3)观察函数图象得到当![]() <x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>
<x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>![]() .
.
试题解析:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),
∴C点坐标为(6,4),
∵点A为线段OC的中点,
∴A点坐标为(3,2),
∴k1=3×2=6,
∴反比例函数解析式为y=![]() ;
;
把x=6代入y=![]() 得y=1,则F点的坐标为(6,1);
得y=1,则F点的坐标为(6,1);
把y=4代入y=![]() 得x=
得x=![]() ,则E点坐标为(
,则E点坐标为(![]() ,4),
,4),
把F(6,1)、E(![]() ,4)代入y=k2x+b得
,4)代入y=k2x+b得
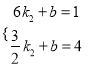 ,
,
解得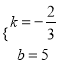 ,
,
∴直线EF的解析式为y=-![]() x+5;
x+5;
(2)△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF
=4×6-![]() ×4×
×4×![]() -
-![]() ×6×1-
×6×1-![]() ×(6-
×(6-![]() )×(4-1)
)×(4-1)
=![]() ;
;
(3)由图象得:不等式k2x+b-![]() >0的解集为
>0的解集为![]() <x<6.
<x<6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=60°.在△ABC的外侧作直线AP,点C关于直线AP的对称点为D,连接AD,BD.
(1)依据题意补全图形;
(2)当∠PAC等于多少度时,AD∥BC?请说明理由;
(3)若BD交直线AP于点E,连接CE,求∠CED的度数;
(4)探索:线段CE,AE和BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.

(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了 分钟追上了正在睡觉的兔子.
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
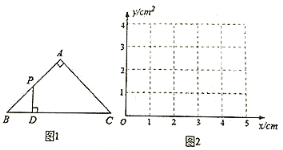
【题目】如图1,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,点P在
,点P在![]() 的边上沿路径
的边上沿路径![]() 移动,过点P作
移动,过点P作![]() 于点D,设
于点D,设![]() ,
,![]() 的面积为
的面积为![]() (当点P与点B或点C重合时,y的值为0).
(当点P与点B或点C重合时,y的值为0).
琪琪根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是琪琪的探究过程,请补充完整:
(1)自变量x的取值范围是______________________;
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y/ | 0 |
| m |
| 2 |
|
| n | 0 |
请直接写出![]() ,
,![]() ;
;
(3)在图2所示的平面直角坐标系![]() 中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像;并结合画出的函数图像,解决问题:当
中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像;并结合画出的函数图像,解决问题:当![]() 的面积为1
的面积为1![]() 时,请直接写出
时,请直接写出![]() 的长度(数值保留一位小数).
的长度(数值保留一位小数).
(4)根据上述探究过程,试写出![]() 的面积为y
的面积为y![]() 与
与![]() 的长度x cm之间的函数关系式,并指出自变量的取值范围.
的长度x cm之间的函数关系式,并指出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
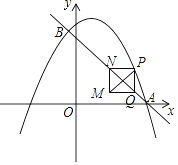
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com