
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
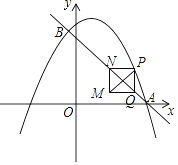
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)m<﹣
;(2)m<﹣![]() 或0<m<3;(3)C=﹣2(m﹣
或0<m<3;(3)C=﹣2(m﹣![]() )2+
)2+![]() ,﹣
,﹣![]() <m<
<m<![]() 且m≠0;(4)m<﹣
且m≠0;(4)m<﹣![]() .
.
【解析】试题分析:(1)先确定出点A,B的坐标,最后用待定系数法即可得出结论。
(2)点P在抛物线上,点Q在直线y=﹣x+3上,点N在直线AB上,设出点P的坐标,再表示出Q、N的坐标,即可得出PN=PQ,再用MN与y轴在PQ的同侧,建立不等式即可得出结论。
(3)点P在点A,B之间的抛物线上,根据(2)可知PQ的长,设正方形PQMN的周长为C,根据C=4PQ,建立C与m的函数关系式,求出其顶点坐标,根据二次函数的性质,即可求得结论。
(4)分两种情况讨论计算即可求出结论。
(1)解:∵直线y=﹣x+3与x轴相交于点A,
∴A(3,0),
∵点B在直线y=﹣x+3上,且B的横坐标为﹣ ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ),
),
∵A,B在抛物线上,
∴ 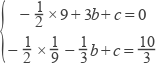 ,
,
∴ ![]()
(2)解:方法1、由(1)知,b= ![]() ,c=
,c= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
设P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),
),
∵点Q在直线y=﹣x+3上,
∴Q(m,﹣m+3),
∵点N在直线AB上,
∴N(( ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ),(﹣
),(﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() )),
)),
∴PN=| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ﹣m|=|
﹣m|=| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() |
|
∴PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ﹣(﹣m+3)|=|﹣
﹣(﹣m+3)|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,
|,
∵四边形PQMN时正方形,
∴PN=PQ,
∴| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() |=|﹣
|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,此时等式恒成立,
|,此时等式恒成立,
当m<0且m≠﹣ ![]() 时,
时,
∵MN与y轴在PQ的同侧,
∴点N在点P右侧,
∴ ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() >m,
>m,
∴m<﹣ ![]() ,
,
当m>0且m≠3时,
∵MN与y轴在PQ的同侧,
∴点P在点N的右侧,
∴ ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() <m,
<m,
∴﹣ ![]() <m<3,
<m<3,
∴0<m<3,
即:m的范围为m<﹣ ![]() 或0<m<3;
或0<m<3;
方法2、如图,
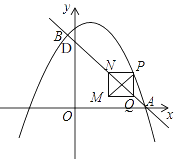
记直线AB与y轴的交点为D,
∵直线AB的解析式为y=﹣x+3,
∴D(0,3),
∴OD=3,
∵A(3,0),
∴OA=3,
∴OA=OB,
∴∠ODA=45°,
∵PQ∥y轴,
∴∠PQB=45°,
记:直线PN交直线AB于N',
∵四边形PQMN是正方形,
∴∠QPN=90°,
∴∠PN'Q=45°=∠PQN',
∴PQ=PN',
∵四边形PQMN是正方形,
∴PQ=PN,
点N在点P的左侧时,点N'都在直线AB上,
∵MN与y轴在PQ的同侧,
∴m的范围为m<﹣ ![]() 或0<m<3
或0<m<3
(3)解:由(1)知,b= ![]() ,c=
,c= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
设P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),
),
∵点Q在直线y=﹣x+3上,
∴Q(m,﹣m+3),
∴PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ﹣(﹣m+3)|=|﹣
﹣(﹣m+3)|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,
|,
∵点P在点A,B之间的抛物线上,
∴PQ=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,(﹣
,(﹣ ![]() <m<3且m≠0),
<m<3且m≠0),
∵设正方形PQMN的周长为C,
∴C=4PQ=4(﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() )=﹣2m2+
)=﹣2m2+ ![]() m+2=﹣2(m﹣
m+2=﹣2(m﹣ ![]() )2+
)2+ ![]() ,
,
∵C随m增大而增大,
∴m< ![]() ,
,
∴﹣ ![]() <m<
<m< ![]() 且m≠0
且m≠0
(4)解:当△PQM与坐标轴有2个公共点时,
∴m<0或0<m<3
当0<m<3,PN>yP ,
由(2)知,P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),PQ=|﹣
),PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |=﹣
|=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]()
∵四边形PQMN是正方形,
∴PN=PQ=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() >﹣
>﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∴m>3,所以,此种情况不符合题意;
当m<0时,PN>yP ,
∵PQ= ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ,
,
∵四边形PQMN是正方形,
∴PN=PQ= ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() >﹣
>﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∴m>3(舍)或m<﹣ ![]() ,
,
即:当△PQM与坐标轴有2个公共点时,m<﹣ ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二 次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四 边形ABCD为1阶准菱形.

(I)判断与推理:
(i)邻边长分别为2和3的平行四边形是_________阶准菱形;
(ii)为了剪去一个菱形,进行如下操作:如图2,把平行四边形ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE,请证明四边形ABFE是菱形.

(Ⅱ)操作与计算:
已知平行四边形ABCD的邻边长分别为l,a(a>1),且是3阶准菱形,请画出平行四边形ABCD及裁剪线的示意图,并在图形下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格纸的格点上.
(1) 画出△ABC关于直线MN的对称图形△![]() ;
;
(2) 画出△ABC关于点O的中心对称图形△![]() ;
;
(3) 画出△ABC绕点B逆时针旋转900后的图形△![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
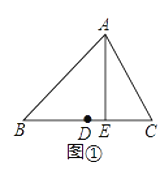
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,易证△ABP∽△PCD,从而得到BPPC=ABCD(不需证明)

探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,结论BPPC=ABCD仍成立吗?请说明理由?
拓展:如图③,在△ABC中,点P是BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ![]() ,CE=3,则DE的长为 .
,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金给50位同学每人购买一件文化衫或一本相册作为纪念品,已知每件文化衫比每本相册贵9元,用200元恰好可以买到2件文化衫和5本相册.
(1)求每件文化衫和每本相册的价格分别为多少元?
(2)有几种购买文化衫和相册的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
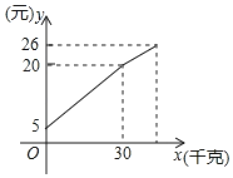
【题目】一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答:
(1)农民自带的零钱是 元;
(2)降价前他每千克土豆出售的价格是 元/千克;列出降价前售出土豆的千克数与他手中持有的钱数(含备用钱)的函数关系式为: ;
(3)降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com