
����Ŀ��һũ���������ǧ���������dz��ۣ�Ϊ�˷��㣬������һЩ����Ǯ���ã����г��۳���һЩ�������ֽ��۳��ۣ��۳�������ǧ�����������г��е�Ǯ����������Ǯ���Ĺ�ϵ��ͼ�����ͼ��ش�
��1��ũ���Դ�����Ǯ�� Ԫ��
��2������ǰ��ÿǧ���������۵ļ۸��� Ԫ/ǧ�ˣ��г�����ǰ�۳�������ǧ�����������г��е�Ǯ����������Ǯ���ĺ�����ϵʽΪ�� ��
��3�����ۺ�����ÿǧ��0.4Ԫ���������꣬��ʱ�����е�Ǯ��������Ǯ����26Ԫ������һ�����˶�������ȥ������ۣ�
���𰸡���1��5����2��0.5��y��0.5x+5����3����һ������45ǧ�ˣ�����ȥ������ۣ�
��������
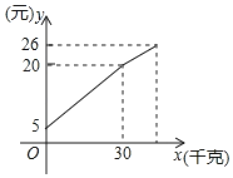
��1��ֱ�Ӹ���ͼ����y��Ľ����֪��ũ���Դ�����Ǯ��5Ԫ��
��2���轵�۳���ǰ��ũ�����е�Ǯ�����۳�������ǧ�����Ĺ�ϵΪ��y=kx+b���ѵ㣨0��5������30��20���������ô���ϵ�����ɵ�y��0.5x+5��
��3���ȸ���������ü��۳��۵���������15ǧ�ˣ��̶��ɵ�����Ϊ45ǧ�ˣ�
�⣺��1����ͼ��ɵã�
ũ���Դ�����Ǯ��5Ԫ��
�ʴ�Ϊ��5��
��2������ǰ��ÿǧ���������۵ļ۸��ǣ���20��5����30��0.5Ԫ/ǧ�ˣ�
�轵��ǰ�۳�������ǧ�����������г��е�Ǯ����������Ǯ���ĺ�����ϵʽΪy��kx+b��
![]() ��ã�
��ã�![]() ��
��
������ǰ�۳�������ǧ�����������г��е�Ǯ����������Ǯ���ĺ�����ϵʽΪy��0.5x+5��
�ʴ�Ϊ��0.5��y��0.5x+5��
��3��30+��26��20����0.4��45��ǧ�ˣ���
����һ������45ǧ�ˣ�����ȥ������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
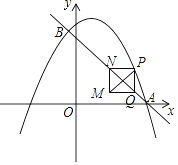
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��x+3��������![]() ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ![]() ������P�����������˶��������A��B�غϣ�������P��y���ƽ���ߣ���ֱ��AB�ڵ�Q����PQ����y���غ�ʱ����PQΪ����������PQMN��ʹMN��y����PQ��ͬ�࣬����PM�����P�ĺ�����Ϊm��
������P�����������˶��������A��B�غϣ�������P��y���ƽ���ߣ���ֱ��AB�ڵ�Q����PQ����y���غ�ʱ����PQΪ����������PQMN��ʹMN��y����PQ��ͬ�࣬����PM�����P�ĺ�����Ϊm��
��1����b��c��ֵ��
��2������N����ֱ��AB��ʱ��ֱ��д��m��ȡֵ��Χ��
��3������P��A��B����֮������������˶�ʱ����������PQMN���ܳ�ΪC����C��m֮��ĺ�����ϵʽ����д��C��m���������ʱm��ȡֵ��Χ��
��4������PQM����������2��������ʱ��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������桷�в�������˺ܶ��µĴʻ㣬Ϊ�˽�ѧ���Ƕ��´ʻ�Ĺ�ע�ȣ�ij��ѧ��ȤС��ѡȡ���е�![]() ����������+�������
����������+�������![]() ��������������
��������������![]() ��������������
�����������С���![]() ������������ʱ�����ĸ��ȴ���ȫУѧ���н����˳���������Ҫ�����ÿλͬѧֻ�ܴ���ѡ��һ�������ע���ȴʣ����ݵ���������С����������µ�������������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ������������⣺
������������ʱ�����ĸ��ȴ���ȫУѧ���н����˳���������Ҫ�����ÿλͬѧֻ�ܴ���ѡ��һ�������ע���ȴʣ����ݵ���������С����������µ�������������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ������������⣺


��1������һ�������˶�����ͬѧ��
��2�����ͳ��ͼ��![]() ��
��![]() ��ֵ��
��ֵ��
��3������ͳ��ͼ�У��ȴ�![]() ��
��![]() ��������ͳ��ͼ��Բ�ĽǷֱ��Ƕ��ٶȣ�
��������ͳ��ͼ��Բ�ĽǷֱ��Ƕ��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ���������У�����ֱ�DZߵij��ȷֱ�Ϊa��b��б�߳���Ϊc����a2��b2��c2��������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ�����˽��۳�Ϊ���ɶ�������һ��ֽ�ϻ�����ͬ����С��ֱ��������ABC��A��B��C�䣬��������ƴ����ͼ��ʾ����״ (��C��A���غϣ�����ֱ�������ε�б���ഹֱ)��������ƴ�õ�ͼ��֤�����ɶ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��Rt��ABC��б��AB�����ڵ�D����ֱ�DZ�AC�ཻ��E��F���㣬����DE����֪��B=30������O�İ뾶Ϊ12����DE�ij���Ϊ4����
��1����֤��DE��BC��
��2����AF=CE�����߶�BC�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��ͼ���ཻ��A��B���㣮����ͼ������
��ͼ���ཻ��A��B���㣮����ͼ������
��1������������һ�κ����Ĺ�ϵʽ��
��2������ͼ��д��ʹ��һ�κ�����ֵ���ڸ÷�����������ֵ��x��ȡֵ��Χ��
��3�������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���ͼ���ڡ�ABC�У�AB=AC��DΪBC��һ�㣬��B=30��������AD��
��1������BAD=45������֤����ACDΪ���������Σ�
��2������ACDΪֱ�������Σ����BAD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˹�ͬ����һ����ʽ�˷���(2x��a)(3x��b)�����ڼ׳����˵�һ������ʽ��a�ķ��ţ��õ��Ľ��Ϊ6x2��11x��10��������©���˵ڶ�������ʽ�е�x��ϵ�����õ��Ľ��Ϊ2x2��9x��10.��������a��b��ֵ���Ƕ��٣���д�������ʽ�˷�����ȷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӹ���ȥij�У��ɳ�����ͨ�г����������֪��������ʻ·����400ǧ�ף���ͨ�г�����ʻ·���Ǹ�������ʻ·�̵�1��3����
��1������ͨ�г�����ʻ·�̣�
��2����������ƽ���ٶ���ǧ��/ʱ������ͨ�г�ƽ���ٶ���ǧ��/ʱ����2��5�����ҳ�����������ʱ��ȳ�����ͨ�г�����ʱ������3Сʱ���������ƽ���ٶ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com