
【题目】在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2,即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A′B′C′,并把它们拼成如图所示的形状 (点C和A′重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.

科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三点分别在CD、AD、BC上,如图所示.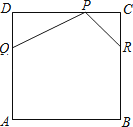
(1)当皮雕师傅切下△PDQ时,若DQ长度为x公分,请你以x表示此时△PDQ的面积.
(2)承(1),当x的值为多少时,五边形PQABR的面积最大?请完整说明你的理由并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点.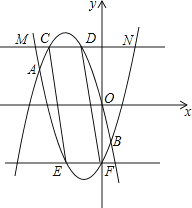
(1)求二次函数y1的解析式;
(2)将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2 , 直线y=m(m>0)交y2于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,y1、y2交于A、B两点,如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与y1、y2的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4 ![]() ,其中正确的结论个数为( )
,其中正确的结论个数为( ) 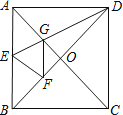
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com