
【题目】如图,已知二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点.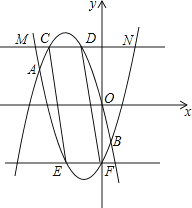
(1)求二次函数y1的解析式;
(2)将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2 , 直线y=m(m>0)交y2于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,y1、y2交于A、B两点,如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与y1、y2的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
【答案】
(1)
解:∵二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点,
∴ ![]() 解得
解得 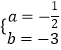 ,
,
∴二次函数y1的解析式y1=﹣ ![]() x2﹣3x
x2﹣3x
(2)
解:∵y1=﹣ ![]() (x+3)2+
(x+3)2+ ![]() ,
,
∴顶点坐标(﹣3, ![]() ),
),
∵将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2,
∴抛物线y2的顶点坐标(﹣1,﹣ ![]() ),
),
∴抛物线y2为y= ![]() (x+1)2﹣
(x+1)2﹣ ![]() ,
,
由 ![]()
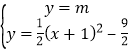 消去y整理得到x2+2x﹣8﹣2m=0,设x1,x2是它的两个根,
消去y整理得到x2+2x﹣8﹣2m=0,设x1,x2是它的两个根,
则MN=|x1﹣x2|= ![]() =
= ![]()
(3)
解:由 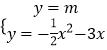 消去y整理得到x2+6x+2m=0,设两个根为x1,x2,
消去y整理得到x2+6x+2m=0,设两个根为x1,x2,
则CD=|x1﹣x2|= ![]() =
= ![]() ,
,
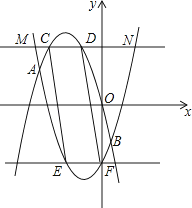
由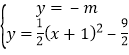
![]() 消去y得到x2+2x﹣8+2m=0,设两个根为x1,x2,
消去y得到x2+2x﹣8+2m=0,设两个根为x1,x2,
则EF=|x1﹣x2|= ![]() =
= ![]() ,
,
∴EF=CD,EF∥CD,
∴四边形CEFD是平行四边形.
【解析】(1)根据待定系数法即可解决问题;
(2)先求出抛物线y2的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN;
(3)用类似(2)的方法,分别求出CD、EF即可解决问题.本题考查二次函数综合题、根与系数关系、平行四边形的判定等知识,解题的关键是灵活应用这些知识解决问题,记住公式|x1﹣x2|= ![]() ,属于中考压轴题.
,属于中考压轴题.
【考点精析】掌握平行四边形的判定是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( ) 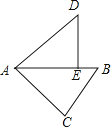
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子有:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β),其中错误的有( )个
(∠α﹣∠β),其中错误的有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2,即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A′B′C′,并把它们拼成如图所示的形状 (点C和A′重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过
统计后绘制了两幅尚不完整的统计图.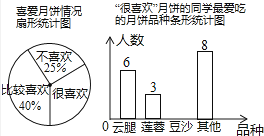
(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为度;条形统计图中,喜欢“豆沙”月饼的学生有人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位得到△A1B1C1 , 再作△A1B1C1关于x轴对称图形△A2B2C2 , 则顶点A2的坐标是________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com