
【题目】∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子有:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β),其中错误的有( )个
(∠α﹣∠β),其中错误的有( )个
A. 1 B. 2 C. 3 D. 4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.
上,AD// BC//y 轴.
(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;
(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;
(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:logab(a>0,a≠1,b>0)表示a,b之间的一种运算.
现有如下的运算法则:lognan=n.logNM= ![]() (a>0,a≠1,N>0,N≠1,M>0).
(a>0,a≠1,N>0,N≠1,M>0).
例如:log223=3,log25= ![]() ,则log1001000=
,则log1001000=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点.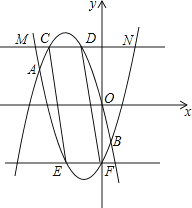
(1)求二次函数y1的解析式;
(2)将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2 , 直线y=m(m>0)交y2于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,y1、y2交于A、B两点,如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与y1、y2的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数y= ![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com