
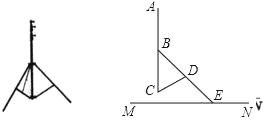
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
【答案】(40+30![]() )cm
)cm
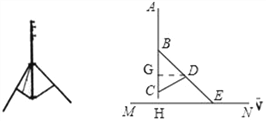
【解析】分析:过点D作DG⊥BC于点G,延长AC交MN于点H,则AH⊥MN,在Rt△DCG中,求出DG的值,在Rt△BDG中,求出BD的值,在Rt△BHE中,求出BH的值,从而结论可求.
详解:过点D作DG⊥BC于点G,延长AC交MN于点H,则AH⊥MN,
在Rt△DCG中,根据sin∠GCD=![]() ,得DG=CDsin∠GCD=
,得DG=CDsin∠GCD=![]() ,
,
在Rt△BDG中,根据sin∠GBD=![]() ,得
,得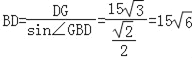 ,
,
∵D为BE的中点,
∴BE=2BD=30![]() ,
,
在Rt△BHE中,根据cos∠HBE=![]() ,
,
得BH=BE![]() ,
,
∴AH=AB+BH=40+30![]() ,
,
∴脚架BE的长度为30![]() cm,支架最高点A到地面
cm,支架最高点A到地面
的距离为(![]() )cm.
)cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
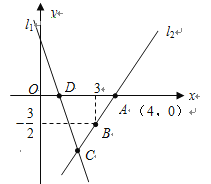
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 与
与![]() 的面积相等,请求出点P的坐标.
的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
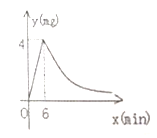
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
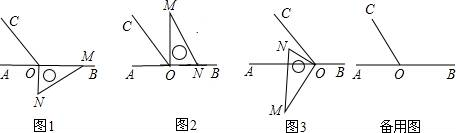
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一次函数y=2x﹣b(b为常数)的图象位于x轴上方的部分沿x轴翻折后,得到的折线是函数y=﹣|2x﹣b|(b为常数)的图象.若该图象在直线y=﹣4上方的点的横坐标x都满足0<x<5.则b的取值范围是( )
A. b≥﹣6 B. b≤4 C. ﹣6≤b≤﹣4 D. 4≤b≤6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为![]() ,另两边长度不变,则点P到原点的最大距离变为______.
,另两边长度不变,则点P到原点的最大距离变为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
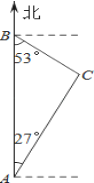
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com