
分析 由方程$\frac{ax+2}{x-4}$=1的解为非负数可得关于a的不等式$-\frac{6}{a-1}$≥0且$-\frac{6}{a-1}$≠4求得a的范围,由式组$\left\{\begin{array}{l}{2x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解可得-1≤$\frac{a}{2}$<0求得a的范围,二者结合可得a的取值范围.
解答 解:解方程$\frac{ax+2}{x-4}$=1得:x=$-\frac{6}{a-1}$,
∵方程的解为非负数,
∴$-\frac{6}{a-1}$≥0且$-\frac{6}{a-1}$≠4,
解得:a<1且a≠-$\frac{1}{2}$,
解不等式2x-a>0,得:x>$\frac{a}{2}$,
解不等式-3+2x≤1,得:x≤2,
∵不等式组有三个整数解,
∴-1≤$\frac{a}{2}$<0,
解得:-2≤a<0,
综上:-2≤a<0且a≠-$\frac{1}{2}$,
故答案为:-2≤a<0且a≠-$\frac{1}{2}$.
点评 本题主要考查解分式方程和解一元一次不等式组及方程的解、不等式组的解,根据方程的解和不等式组的整数解得出关于a的不等式是解题的关键.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
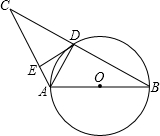 如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E连接AD,则下列结论正确的个数是( )
如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E连接AD,则下列结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com