
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据分式混合运算的法则对各小题进行逐一计算即可.
解答 解:①∵A=$\frac{4}{{x}^{2}-4}$,B=$\frac{1}{x+2}$+$\frac{1}{2-x}$,
∴B=$\frac{1}{x+2}$-$\frac{1}{x-2}$=$\frac{x-2-x-2}{(x+2)(x-2)}$=$\frac{-4}{{x}^{2}-4}$,
∴A≠B,故本小题错误;
②∵A•B=$\frac{4}{{x}^{2}-4}$•($\frac{1}{x+2}$-$\frac{1}{x-2}$)=$\frac{4}{{x}^{2}-4}$•$\frac{-4}{{x}^{2}-4}$=-$\frac{16}{{(x}^{2}-4)^{2}}$,
∴A•B≠1,故本小题错误;
③∵A+B=$\frac{4}{{x}^{2}-4}$+$\frac{-4}{{x}^{2}-4}$=0,
∴A+B=0,故本小题正确.
故选B.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
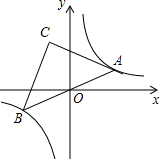 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=$\frac{8}{x}$ | B. | y=$\frac{16}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=-$\frac{8}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面的证明(在括号中注明理由).
完成下面的证明(在括号中注明理由).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com