
在平面直角坐标系xOy中,抛物线y=x2﹣(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,﹣1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.

解:(1)∵y=x2﹣(m+n)x+mn=(x﹣m)(x﹣n),
∴x=m或x=n时,y都为0,
∵m>n,且点A位于点B的右侧,
∴A(m,0),B(n,0).
∵m=2,n=1,
∴A(2,0),B(1,0).
(2)∵抛物线y=x2﹣(m+n)x+mn(m>n)过C(0,﹣1),
∴﹣1=mn,
∴n=﹣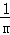 ,
,
∵B(n,0),
∴B(﹣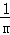 ,0).
,0).
∵AO=m,BO=﹣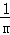 ,CO=1
,CO=1
∴AC=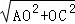 =
=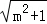 ,
,
BC=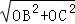 =
=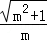 ,
,
AB=AO+BO=m﹣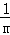 ,
,
∵(m﹣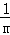 )2=(
)2=(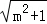 )2+(
)2+(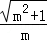 )2,
)2,
∴AB2=AC2+BC2,
∴∠ACB=90°.
(3)∵A(m,0),B(n,0),C(0,mn),且m=2,
∴A(2,0),B(n,0),C(0,2n).
∴AO=2,BO=|n|,CO=|2n|,
∴AC=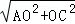 =
=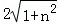 ,
,
BC=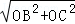 =
=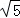 |n|,
|n|,
AB=xA﹣xB=2﹣n.
①当AC=BC时,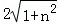 =
=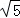 |n|,解得n=2(A、B两点重合,舍去)或n=﹣2;
|n|,解得n=2(A、B两点重合,舍去)或n=﹣2;
②当AC=AB时,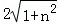 =2﹣n,解得n=0(B、C两点重合,舍去)或n=﹣
=2﹣n,解得n=0(B、C两点重合,舍去)或n=﹣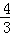 ;
;
③当BC=AB时,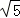 |n|=2﹣n,
|n|=2﹣n,
当n>0时,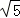 n=2﹣n,解得n=
n=2﹣n,解得n=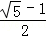 ,
,
当n<0时,﹣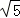 n=2﹣n,解得n=﹣
n=2﹣n,解得n=﹣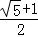 .
.
综上所述,n=﹣2,﹣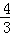 ,﹣
,﹣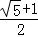 ,
,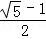 时,△ABC是等腰三角形.
时,△ABC是等腰三角形.


科目:初中数学 来源: 题型:
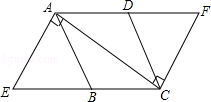
如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )
|
| A. | 22 | B. | 18 | C. | 14 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA•OB﹣3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列叙述正确的是( )
|
| A. | 方差越大,说明数据就越稳定 |
|
| B. | 在不等式两边同乘或同除以一个不为0的数时,不等号的方向不变 |
|
| C. | 不在同一直线上的三点确定一个圆 |
|
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:
甲班:  乙班:
乙班:
| 等级 | 成绩(S ) | 频数 |
| A | 90<S≤100 | x |
| B | 80<S≤90 | 15 |
| C | 70<S≤80 | 10 |
| D | S≤70 | 3 |
| 合计 | 30 |
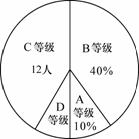
第19题图
根据上面提供的信息回答下列问题
⑴(3分)表中x= ,甲班学生成绩的中位数落在等级 中,扇形统计图中等级D部分的扇形圆心角n= .
⑵(5分)现学校决定从两班所有A等级成绩的学生中随机抽取2名同学参加市级征文比赛.求抽取到两名学生 恰好来自同一班级的概率(请列树状图或列表求解).
恰好来自同一班级的概率(请列树状图或列表求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com