
已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA•OB﹣3,求k的值.
科目:初中数学 来源: 题型:
如图,在半径为6cm的⊙O中,点A是劣弧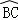 的中点,点D是优弧
的中点,点D是优弧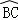 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6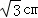 ;③sin∠AOB=
;③sin∠AOB=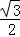 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )

|
| A. | ①③ | B. | ①②③④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
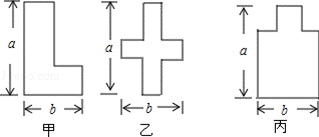
某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
|
| A. | 甲种方案所用铁丝最长 | B. | 乙种方案所用铁丝最长 |
|
| C. | 丙种方案所用铁丝最长 | D. | 三种方案所用铁丝一样长 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,抛物线y=x2﹣(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,﹣1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com