
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是 ![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 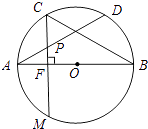
(1)求∠ABC的度数;
(2)若CM=4 ![]() ,求
,求 ![]() 的长度.(结果保留π)
的长度.(结果保留π)
【答案】
(1)解:如图,连接BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠DAB=30°,
∴∠ABD=90°﹣30°=60°.
∵C是 ![]() 的中点,
的中点,
∴∠ABC=∠DBC= ![]() ∠ABD=30°
∠ABD=30°

(2)解:如图,连接OC,则∠AOC=2∠ABC=60°,
∵CM⊥直径AB于点F,
∴CF= ![]() CM=2
CM=2 ![]() .
.
∴在Rt△COF中,CO= ![]() CF=
CF= ![]() ×2
×2 ![]() =4,
=4,
∴ ![]() 的长度为
的长度为 ![]() =
= ![]() .
.

【解析】(1)连接BD,根据AB为⊙O的直径,求出∠ADB=90°,得到∠ABD=60°,再根据C是 ![]() 的中点,求出∠ABC的度数;(2)连接OC,则∠AOC=2∠ABC=60°,求出CO的长,即可求出
的中点,求出∠ABC的度数;(2)连接OC,则∠AOC=2∠ABC=60°,求出CO的长,即可求出 ![]() 的长度.
的长度.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆心角、弧、弦的关系的理解,了解在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)若a∶b=3∶4,c=75cm,求a、b;
(2)若a∶c=15∶17,b=24,求△ABC的面积;
(3)若c-a=4,b=16,求a、c;
(4)若∠A=30°,c=24,求c边上的高hc;
(5)若a、b、c为连续整数,求a+b+c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲仓库有水泥100吨,乙仓库有水泥80吨,要全部运动A、B两工地,已知A工地需要70吨,B工地需要110吨,甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨,乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨,本次运送水泥总运费需要25900元,问甲仓库运到A工地水泥的吨数.(运费:元/吨,表示运送每吨水泥所需的人民币)
(1)设甲仓库运到A工地水泥的吨数为x吨,请在下面表格中用x表示出其他未知量.
甲仓库 | 乙仓库 | |
A工地 | x |
|
B工地 |
| x+10 |
(2)用含x的代数式表示运送甲仓库100吨水泥的运费为 元.(写出化简后的结果)
(3)请根据题目中的等量关系和以上的分析列出方程.(只列出方程即可,写成ax+b=0的形式,不用解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、 ![]() 、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 .
、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
![]()
A. P B. R C. Q D. T
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(+4)×(-5); (2)(-0.125)×(-8);
(3)(-2![]() )×(-
)×(-![]() ); (4)0×(-13.52);
); (4)0×(-13.52);
(5)(-3.25)×(+![]() ); (6)(-1)×a.
); (6)(-1)×a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将一张长方形的纸片连续对折,对折时每次折痕与上次的折痕保持平行,对折一次得到1条折痕(图中虚线),对折二次得到3条折痕,对折三次得到7条折痕,那么对折2018次后可以得到________条折痕.

查看答案和解析>>
科目:初中数学 来源: 题型:
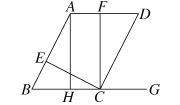
【题目】如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com