
【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,
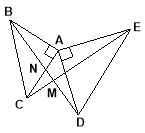
证明:(1)BD=CE. (2)BD⊥CE.
【答案】略
【解析】(1)要证明BD=CE,只要证明△ABD≌△ACE即可,两三角形中,已知的条件有AD=AE,AB=AC,那么只要再得出两对应边的夹角相等即可得出三角形全等的结论.我们发现∠BAD和∠EAC都是90°加上一个∠CAD,因此∠CAE=∠BAD.由此构成了两三角形全等中的(SAS)因此两三角形全等.
(2)要证BD⊥CE,只要证明∠BMC是个直角就行了.由(1)得出的全等三角形我们可知:
∠ABN=∠ACE,三角形ABC中,∠ABN+∠CBN+∠BCN=90°,根据上面的相等角,我们可得出∠ACE+∠CBN+∠BCN=90°,即∠ABN+∠ACE=90°,因此∠BMC就是直角了.


科目:初中数学 来源: 题型:
【题目】综合题
(1)用适当的方法解方程:
①(x﹣2)2=2x﹣4
②x2﹣2x﹣8=0.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣a+1),其中a是方程x2﹣x=6的根.
﹣a+1),其中a是方程x2﹣x=6的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是 ![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 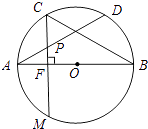
(1)求∠ABC的度数;
(2)若CM=4 ![]() ,求
,求 ![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
计算:![]() .
.
解法一:原式=
![]()
解法二:原式=(-![]() )÷[(
)÷[(![]() )-(
)-(![]() )]=
)]=![]() ÷
÷![]() =-
=-![]() ×3=-
×3=-![]() .
.
解法三:原式的倒数为(![]() )÷(-
)÷(-![]() )=
)=![]() ×(-30)-
×(-30)-![]() ×(-30)+
×(-30)+![]() ×(-30)-
×(-30)-![]() ×(-30)=-20+3-5+12=-10,
×(-30)=-20+3-5+12=-10,
故原式=-![]() .
.
(1)上述解法得出的结果不同,肯定有错误的解法,你认为解法________是错误的,在正确的解法中,你认为解法________最简捷;
(2)利用(1)中你认为最简捷的解法计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法——更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也,以等数约之.”意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数:
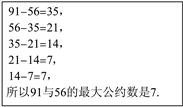
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?
(4)你认为可用什么办法求数轴上两点之间的距离?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.
(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,此时线段
,此时线段 ![]() 的长是 . 现将三角板
的长是 . 现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)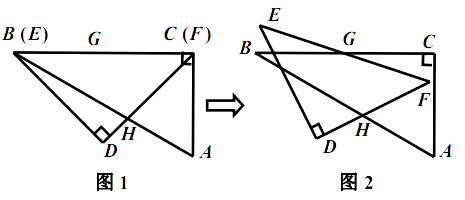
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com