练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

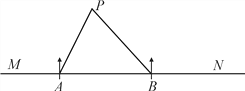
    【题目】超速行驶是一种十分危险的违法驾驶行为，在一条东西走向的笔直高速公路MN上，小型车限速为每小时100千米. 现有一辆小汽车行驶到A处时，发现北偏东30°方向200米处有一超速监测仪P. 10秒后，小汽车行驶至B处，测得监测仪P在B处的北偏西45°方向上. 请问：这辆车超速了吗？通过计算说明理由．（参考数据：）

    【答案】这辆车没有超速

    【解析】分析：过点P作PC⊥AB于C，根据Rt△APC的性质求出AC和PC的长度，根据等腰三角形的性质得出BC的长度，从而得出AB的长度，最后根据速度的计算公式求出速度，从而得出答案．

    详解：过点P作PC⊥AB于C，

    ，由题可知：， ，

    ∴在中， ， ，

    在中，， ∴

    ，

    ，所以这辆车没有超速．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在Rt△ABO中，∠B=90°，∠OAB=30°，OA=3．以点O为原点，斜边OA所在直线为x轴，建立平面直角坐标系，以点P（4，0）为圆心，PA长为半径画圆，⊙P与x轴的另一交点为N，点M在⊙P上，且满足∠MPN=60°．⊙P以每秒1个单位长度的速度沿x轴向左运动，设运动时间为ts，解答下列问题：

    （发现）（1）的长度为多少；

    （2）当t=2s时，求扇形MPN（阴影部分）与Rt△ABO重叠部分的面积．

    （探究）当⊙P和△ABO的边所在的直线相切时，求点P的坐标．

    （拓展）当与Rt△ABO的边有两个交点时，请你直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

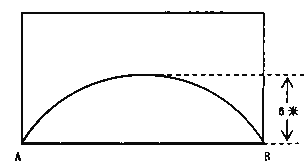
    【题目】为了实现省城合肥跨越发展，近两年我市开始全面实施“畅通一环”工程，如图为一环路的一座下穿路拱桥，它轮廓是抛物线，桥的跨度AB=16米，拱高为6米.

    （1）请以A点为坐标原点，AB所在直线为x轴建立平面直角坐标系，将抛物线放在直角坐标系中，求出抛物线的解析式；

    （2）若桥拱下是双向行车道，其中一条行车道能否并排行驶宽3米，高2米的两辆汽车（汽车间隔不小于1米）说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

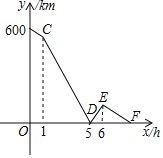
    【题目】A、B两地之间为直线距离且相距600千米，甲开车从A地出发前往B地，乙骑自行车从B地出发前往A地，已知乙比甲晚出发1小时，两车均匀速行驶，当甲到达B地后立即原路原速返回，在返回途中再次与乙相遇后两车都停止，如图是甲、乙两人之间的距离s（千类）与甲出发的时间t（小时）之间的图象，则当甲第二次与乙相遇时，乙离B地的距离为_____千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

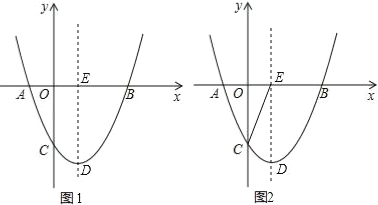
    【题目】如图1，已知二次函数y＝ax2+bx+c(a≠0)的图象与x轴交于A(﹣1，0)，B(3，0)两点，与y轴交于点C(0，﹣2)，顶点为D，对称轴交x轴于点E．

    (1)求该二次函数的解析式；

    (2)设M为该抛物线对称轴左侧上的一点，过点M作直线MN∥x轴，交该抛物线于另一点N．是否存在点M，使四边形DMEN是菱形？若存在，请求出点M的坐标；若不存在，请说明理由；

    (3)连接CE(如图2)，设点P是位于对称轴右侧该抛物线上一点，过点P作PQ⊥x轴，垂足为Q．连接PE，请求出当△PQE与△COE相似时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将两个圆形纸片（半径都为1）如图重叠水平放置，向该区域随机投掷骰子，则骰子落在重叠区域（阴影部分）的概率大约为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在创建“全国文明城市”和“省级文明城区”过程中，栾城区污水处理厂决定先购买A、B两型污水处理设备共20台，对城区周边污水进行处理．已知每台A型设备价格为12万元，每台B型设备价格为10万元；1台A型设备和2台B型设备每周可以处理污水640吨，2台A型设备和3台B型设备每周可以处理污水1080吨．

    （1）求A、B两型污水处理设备每周分别可以处理污水多少吨？

    （2）要想使污水处理厂购买设备的资金不超过230万元，但每周处理污水的量又不低于4500吨，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一块形状如图所示的玻璃，不小心把DEF部分打碎，现在只测得AB=60cm，BC=80cm，∠A=120°，∠B=60°，∠C=150°，你能设计一个方案，根据测得的数据求出AD的长吗？

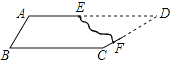
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等边△ABC，AB=16，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．

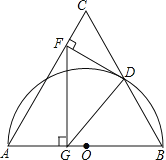
    （1）求证：DF是⊙O的切线；

    （2）求FG的长；

    （3）求tan∠FGD的值．

    查看答案和解析>>

    同步练习册答案