
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ߶ȷ�չ���ݵ��飬��ɳ��ij��С�͡���ѧ��������ҵ���Ŀ�ݹ�˾���������·������·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
��1����ÿ�ݹ�˾Ͷ���ܼ�������ƽ�������ʣ�
��2�����ƽ��ÿ��ÿ������Ͷ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ���ɽ���6�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
���𰸡���1��10%����2��������Ҫ����2��ҵ��Ա��
��������
�����������1����ÿ�ݹ�˾Ͷ���ܼ�������ƽ��������Ϊx�����ݡ��������·������·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ���������̣��ⷽ�̼��ɣ�
��2�������������6�·ݵĿ��Ͷ�����������21�����Ͷ��ҵ��Ա����ɵĿ��Ͷ�����Ƚϵó��ù�˾������ɽ���6�·ݵĿ��Ͷ�����������������Ҫ����ҵ��Ա��������
�����������1����ÿ�ݹ�˾Ͷ���ܼ�������ƽ��������Ϊx�������������
![]() �����
�����![]() =0.1��
=0.1��![]() =��2.1������������ȥ����
=��2.1������������ȥ����
�𣺸ÿ�ݹ�˾Ͷ���ܼ�������ƽ��������Ϊ10%��
��2������6�·ݵĿ��Ͷ��������12.1����1+10%��=13.31���������
��ƽ��ÿ��ÿ������Ͷ��0.6�������21�����Ͷ��ҵ��Ա����ɵĿ��Ͷ�������ǣ�0.6��21=12.6��13.31����ù�˾���е�21�����Ͷ��ҵ��Ա������ɽ���6�·ݵĿ��Ͷ������
����Ҫ����ҵ��Ա��13.31��12.6����0.6=![]() ��2���ˣ���
��2���ˣ���
�𣺸ù�˾���е�21�����Ͷ��ҵ��Ա������ɽ���6�·ݵĿ��Ͷ������������Ҫ����2��ҵ��Ա��


 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M=x2��8x+22��N=��x2��8x��3����ôM��N�Ĵ�С��ϵ�ǣ� ��
A.M��N
B.M=N
C.M��N
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O��ֱ��AB�ϵ�һ�㣬OC��OD������ΪO.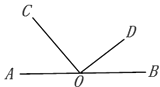
��1������BOD=32�㣬���AOC�Ķ�����
��2������AOC����BOD=2:1��ֱ��д����BOD�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ3�ĵȱߡ�ABC�ı�AB��һ��P����PE��AC��E��QΪBC�ӳ�����һ�㣬��CQ=PA������PQ��AC�ڵ�D����DE�ij�Ϊ�� �� 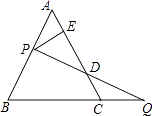
A.1
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ҫ�ڹ涨��ʱ���ڼӹ�100�����������Ч�ʦ���ʱ��t֮��Ĺ�ϵ�У�����˵����ȷ���ǣ� ��
A.��100�ͦǣ�t���DZ���
B.��100�ͦǶ��dz���
C.�Ǻ�t�DZ���
D.��100��t���dz���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������a��4��2+|b��6|=0������a��bΪ�߳��ĵ��������ε��ܳ�Ϊ��������
A. 14 B. 16 C. 13 D. 14��16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=20cm��DE��ֱƽ��AB������ΪE����AC��D������DBC���ܳ�Ϊ35cm����BC�ij�Ϊ�� �� 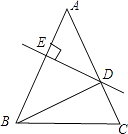
A.5cm
B.10cm
C.15cm
D.17.5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
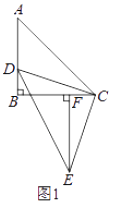
����Ŀ����ABCΪ����ֱ�������Σ���ABC=90�㣬��D��AB���ϣ������A��B�غϣ�����CDΪ��������ֱ�ǡ�CDE����DCE=90�㣮
��1����ͼ1����EF��BC��F����֤����DBC�ա�CFE��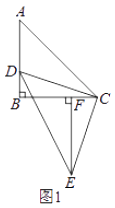
��2����ͼ1�У�����AE��BC��M���� ![]() ��ֵ��
��ֵ��
��3����ͼ2������E��EH��CE��CB���ӳ����ڵ�H������D��DG��DC����AC�ڵ�G������GH������D�ڱ�AB���˶�ʱ��ʽ�� ![]() ��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵�����ɣ�
��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵�����ɣ�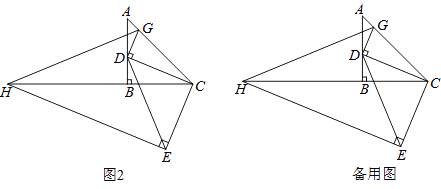
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com