
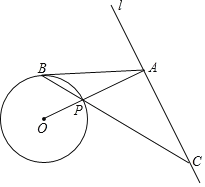
【题目】如图,已知直线l与⊙O无公共点,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若BP=2![]() ,sin∠ACB
,sin∠ACB![]() ,求AB的长.
,求AB的长.
【答案】(1)证明见解析;(2)AB![]() .
.
【解析】
(1)连结OB,根据等腰三角形的性质、对顶角相等证明∠OBA=90°,根据切线的判定定理证明即可;
(2)作直径BD,连接PD,则∠BPD=90°,根据圆周角定理得出△PBD是直角三角形,进而求得![]() ,即为直角三角形求得直径BD,根据
,即为直角三角形求得直径BD,根据![]() ,得到
,得到![]() ,然后设
,然后设![]() ,则
,则![]() ,在
,在![]() 中,根据勾股定理得到
中,根据勾股定理得到![]() ,解得x的值,即可求得AB的长.
,解得x的值,即可求得AB的长.
(1)连结OB,如图1.
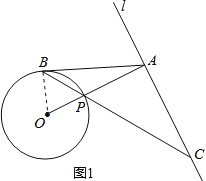
∵AB=AC,
∴∠ABC=∠ACB.
∵OA⊥l,
∴∠ACB+∠APC=90°.
∵OB=OP,
∴∠OBP=∠OPB.
∵∠OPB=∠APC,
∴∠OBP+∠ACB=90°,
∴∠OBP+∠ABC=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)作直径BD,连接PD,则∠BPD=90°,如图2.
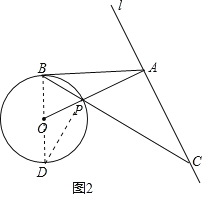
∵AB是⊙O的切线,
∴∠ABC=∠D.
∵∠ABC=∠ACB,
∴∠D=∠ABC=∠ACB.
∵sin∠ACB![]() ,
,
∴sin∠D![]() ,
,
∵BP=2![]() ,
,
∴BD=10,
∴OB=OP=5.
∵sin∠ACB![]() ,
,
∴![]() ,
,
设PA=![]() ,则PC=
,则PC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
设PA=x,则AB=AC=2x,
在Rt△AOB中,AB=2x,OB=5,OA=5+x,
∴(2x)2+52=(5+x)2,
解得:x![]() ,
,
∴AB=2x![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.

(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小雪设计的“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
![]()
已知:线段AB.
求作:以AB为斜边的一个等腰直角△ABC.
作法:
(1)分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于P、Q两点;
AB的长为半径作弧,两弧相交于P、Q两点;
(2)作直线PQ,交AB于点O;
(3)以O为圆心,OA的长为半径作圆,交直线PQ于点C;
(4)连接AC,BC.
则△ABC即为所求作的三角形.根据小雪设计的尺规作图过程:
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明:
证明:∵PA=PB,QA=QB,∴PQ垂直平分AB( )
在⊙O中,
∵AB为直径,∴∠ACB=90°( )
又∵∠AOC=∠BOC=90°,∴AC=BC( ),∴△ABC为以AB为斜边的等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程y(单位:米)与时间t(单位:分)之间的函数关系式如图所示,根据图中提供的信息,有下列说法:①甲队比乙队提前0.5分到达终点②当划行1分钟时,甲队比乙队落后50米③当划行![]() 分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
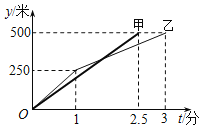
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
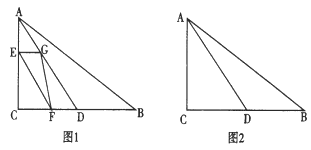
【题目】如图1,△ABC中,∠ACB=90°,AC=4cm,BC=6cm,D是BC的中点.点E从A出发,以acm/s(a>0)的速度沿AC匀速向点C运动;点F同时以1cm/s的速度从点C出发,沿CB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点E作AC的垂线,交AD于点G,连接EF,FG,设它们运动的时间为t秒(t≥t0).
(1)若t=2,△CEF∽△ABC,求a的值;
(2)当a=![]() 时,以点E、F、D、G为顶点点四边形时平行四边形,求t的值;
时,以点E、F、D、G为顶点点四边形时平行四边形,求t的值;
(3)若a=2,是否存在实数t,使得点△DFG是直角三角形?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
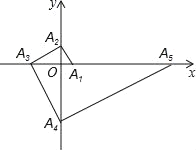
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2垂足为A2,交x轴于点A3过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4,过点A4作A4A5⊥A3A4,垂足为A4…交x轴于点A5:过点A5作A5A6⊥A4A5,A5A6⊥A4A5垂足为A5,交y轴于点A6…按此规律进行下去,则点A2019的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
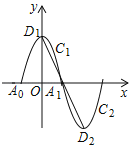
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com