
����Ŀ��������Сѩ��Ƶġ�������֪�߶�Ϊб�ߵĵ���ֱ�������Ρ��ij߹���ͼ���̣�
![]()
��֪���߶�AB��
��������ABΪб�ߵ�һ������ֱ�ǡ�ABC��
������
��1���ֱ��Ե�A�͵�BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶�����������ཻ��P��Q���㣻
AB�ij�Ϊ�뾶�����������ཻ��P��Q���㣻
��2����ֱ��PQ����AB�ڵ�O��
��3����OΪԲ�ģ�OA�ij�Ϊ�뾶��Բ����ֱ��PQ�ڵ�C��
��4������AC��BC��
���ABC��Ϊ�������������Σ�����Сѩ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�油ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤������PA=PB��QA=QB����PQ��ֱƽ��AB�� ��
�ڡ�O�У�
��ABΪֱ�������ACB=90�㣨 ��
�֡ߡ�AOC=��BOC=90�㣬��AC=BC�� �������ABCΪ��ABΪб�ߵĵ���ֱ�������Σ�
���𰸡���1���𰸼���������2�����߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϣ�ֱ������Բ�ܽ���ֱ�ǣ���ȵ�Բ�Ľ����ԵĻ���ȡ����Ե�����ȣ�
��������
(1)��������������ֱ�ߺ�Բ�油ȫͼ�Σ�
(2)������ͼ���̼������֤����
(1)��ͼ��Ϊ��ȫ��ͼ�Σ�

(2)��������֤����
֤������PA=PB��QA=QB��
��PQ��ֱƽ��AB(���߶������˵������ȵĵ��������߶εĴ�ֱƽ������)
�ڡ�O�У�
��ABΪֱ����
���ACB=90�� (ֱ������Բ�ܽ���ֱ��)
�֡ߡ�AOC=��BOC=90�㣬
��AC=BC(��ȵ�Բ�Ľ����ԵĻ���ȡ����Ե������)��
���ABCΪ��ABΪб�ߵĵ���ֱ�������Σ�
�ʴ�Ϊ�����߶������˵������ȵĵ��������߶εĴ�ֱƽ�����ϡ�
ֱ������Բ�ܽ���ֱ�ǡ���ȵ�Բ�Ľ����ԵĻ���ȡ����Ե�����ȣ�


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
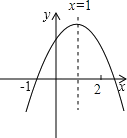
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���Գ���Ϊx=1�������㣨-1��0���������н��ۣ���abc��0����a+c��b����3a+c=0����a+b��m��am+b��������m��1��������ȷ�Ľ����У�������
A. 1��
B. 2��
C. 3��
D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
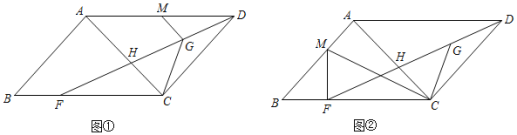
����Ŀ����ͼ��ABCD�У�DFƽ�֡�ADC��AC�ڵ�H��GΪDH���е㣮
��1����ͼ������MΪAD���е㣬AB��AC��AC��9��CF��8��CG��2![]() ����GM��
����GM��
��2����ͼ����MΪ�߶�AB��һ�㣬����MF�������MCD����BCG����MFB����BAC����֤��MC��2CG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
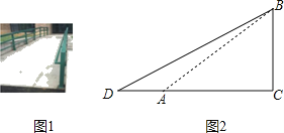
����Ŀ��ͼ1�����ϰ�ͨ����ͼ2�������ʾ��ͼ����֪�½ǡ�BAC=30����б��AB=4m����ACB=90������Ҫ��������и��죬ʹ�������½ǡ�BDC=26.5������Ҫ��ˮƽ����AC���Ӷ���m�������ȷ��0.1�������ο����ݣ�![]() ��1.73��sin26.5���0.45��cos26.5���0.90��tan26.5���0.50��
��1.73��sin26.5���0.45��cos26.5���0.90��tan26.5���0.50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������![]() ��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
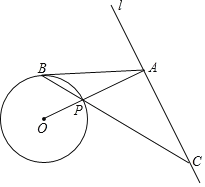
����Ŀ����ͼ����ֱ֪��l���O�����㣬OA��l�ڵ�A������O�ڵ�P����B�ǡ�O��һ�㣬����BP���ӳ���ֱ��l�ڵ�C��ʹ��AB=AC��
��1����֤��AB�ǡ�O�����ߣ�
��2����BP=2![]() ��sin��ACB
��sin��ACB![]() ����AB�ij���
����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x����m��x��m��4ʱ������ʽax2+bx+4a+1��ֵ��ȣ���m��2������1��x��2ʱ������x��ֵ��ʹ����ʽax2+bx+4a+1��ֵΪ3����a��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����ͬѧ����Ϸ����Ϸ�����ǣ���һ�������ĺ��ӣ�����װ�����ź쿨Ƭ�������̿�Ƭ����Ƭ����ɫ����������ͬ�������Ⱥ�Ӻ�����ȡ��һ�ſ�Ƭ�����Żأ�����������ȡ��Ƭ����ɫ��ͬ����С����ʤ������С����ʤ��
��1�����û���״ͼ���б����г���Ϸ���п��ܵĽ����
��2���������ļ�����˵����Ϸ�Ƿ�ƽ��������ƽ������Ϊ��˭������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ͼ�ij�ز�ר���������ij���ز��������Ϊÿǧ��40Ԫ������ÿǧ��60Ԫ���ۣ���ƽ��ÿ����۳�100ǧ�ˣ����������г����鷢�֣�����ÿ����3Ԫ��ƽ��ÿ�������������30ǧ�ˣ���ר�������������ز���Ҫƽ��ÿ�����2240Ԫ�������������ܴ���ÿǧ���ز�Ӧ���۶���Ԫ?
(1)����1:��ÿǧ���ز�Ӧ����xԪ�������⣬�÷���Ϊ��___.
����2:��ÿǧ���ز����ۺ�ΪxԪ�������⣬�÷���Ϊ��___.
(2)����ѡ��һ�ַ�����ɽ��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com